
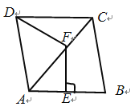
【題目】如圖,菱形![]() 的邊
的邊![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .當
.當![]() 時,則
時,則![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
連接BF,根據菱形的對角線平分一組對角線可得∠BAC=50°,根據線段垂直平分線上的點到兩端點的距離相等可得AF=BF,根據等邊對等角可得∠FBA=∠FAB,再根據菱形的鄰角互補求出∠ABC,然后求出∠CBF,最后根據菱形的對稱性可得∠CDF=∠CBF.
解:如圖,連接BF,
在菱形ABCD中,∠BAC=![]() ∠BAD=
∠BAD=![]() ×100°=50°,
×100°=50°,
∵EF是AB的垂直平分線,
∴AF=BF,
∴∠FBA=∠FAB=50°,
∵菱形ABCD的對邊AD∥BC,
∴∠ABC=180°-∠BAD=180°-100°=80°,
∴∠CBF=∠ABC-∠ABF=80°-50°=30°,
由菱形的對稱性,∠CDF=∠CBF=30°.
故選:B.



 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 和一次函數
和一次函數![]() .
.
(1)當t=0時,試判斷二次函數![]() 的圖象與x軸是否有公共點,如果有,請寫出公共點的坐標;
的圖象與x軸是否有公共點,如果有,請寫出公共點的坐標;
(2)若二次函數![]() 的圖象與x軸的兩個不同公共點,且這兩個公共點間的距離為8,求t的值;
的圖象與x軸的兩個不同公共點,且這兩個公共點間的距離為8,求t的值;
(3)求證:不論實數t取何值,總存在實數x,使![]() ≥
≥![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,O為坐標原點,直線y=kx﹣2k(k<0)的與y軸交于點A,與x軸交于點B.
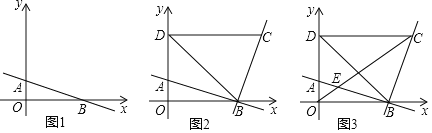
(1)如圖1,求點B的坐標;
(2)如圖2,第一象限內的點C在經過B點的直線y=-![]() x+b上,CD⊥y軸于點D,連接BD,若S△ABD=2k+2,求C點的坐標(用含k的式子表示);
x+b上,CD⊥y軸于點D,連接BD,若S△ABD=2k+2,求C點的坐標(用含k的式子表示);
(3)如圖3,在(2)的條件下,連接OC,交直線AB于點E,若3∠ABD﹣∠BCO=45°,求點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中.直線y=﹣x+3與x軸交于點B,與y軸交于點C,拋物線y=ax2+bx+c經過B,C兩點,與x軸負半軸交于點A,連結AC,A(-1,0)
(1)求拋物線的解析式;
(2)點P(m,n)是拋物線上在第一象限內的一點,求四邊形OCPB面積S關于m的函數表達式及S的最大值;
(3)若M為拋物線的頂點,點Q在直線BC上,點N在直線BM上,Q,M,N三點構成以MN為底邊的等腰直角三角形,求點N的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
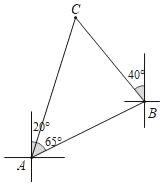
【題目】如圖,一艘船由A港沿北偏東65°方向航行90![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏東20°方向,求A,C兩港之間的距離.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏東20°方向,求A,C兩港之間的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】廊橋是我國古老的文化遺產.如圖,是某座拋物線型的廊橋示意圖,已知拋物線的函數表達式為![]() ,為保護廊橋的安全,在該拋物線上距水面
,為保護廊橋的安全,在該拋物線上距水面![]() 高為8米的點
高為8米的點![]() 、
、![]() 處要安裝兩盞警示燈,則這兩盞燈的水平距離
處要安裝兩盞警示燈,則這兩盞燈的水平距離![]() 是____米.
是____米.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小琴和小江參加學校舉行的“經典誦讀"比賽活動,誦讀材料有《論語》,《三字經》,《弟子規》(分別用字母![]() 依次表示這三個誦讀材料),將
依次表示這三個誦讀材料),將![]() 這三個字母分別寫在
這三個字母分別寫在![]() 張完全相同的不透明卡片的正面上,把這
張完全相同的不透明卡片的正面上,把這![]() 張卡片背面朝上洗勻后放在桌面上,比賽時小琴先從中隨機抽取一張卡片, 記錄下卡精上的內容,放回后洗勻,再由小江從中隨機抽取一張卡片,選手按各自抽取的卡片上的內容進行誦讀比賽.
張卡片背面朝上洗勻后放在桌面上,比賽時小琴先從中隨機抽取一張卡片, 記錄下卡精上的內容,放回后洗勻,再由小江從中隨機抽取一張卡片,選手按各自抽取的卡片上的內容進行誦讀比賽.
![]() 小琴誦讀《論語》的概率是 .
小琴誦讀《論語》的概率是 .
![]() 請用列表法或畫樹狀圖(樹形圖)法求小琴和小江誦讀兩個不同材料的概率.
請用列表法或畫樹狀圖(樹形圖)法求小琴和小江誦讀兩個不同材料的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙M的半徑為4,圓心M的坐標為(6,8),點P是⊙M上的任意一點,PA⊥PB,且PA、PB與x軸分別交于A、B兩點,若點A、點B關于原點O對稱,則AB的最小值為____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,反比例函數![]() (k≠0)的圖象經過點A(1,2)和B(2,n),
(k≠0)的圖象經過點A(1,2)和B(2,n),
(1)以原點O為位似中心畫出△A1B1O,使![]() =
=![]() ;
;
(2)在y軸上是否存在點P,使得PA+PB的值最小?若存在,求出P的坐標;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com