
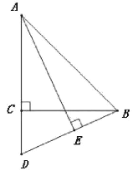
【題目】如圖,在△ABC中,AC=BC,∠ACB=90°,D為AC延長線上一點,連接BD,AE⊥BD于點E.
(1)記△ABC得外接圓為⊙0,
①請用文字描述圓心0的位置;
②求證:點E一定在⊙0上.
(2)將射線AE繞點A順時針旋轉45°后,所得到的射線與BD延長線交于點F,連接CF,CE.
①依題意補全圖形;
②用等式表示線段AF,CE,BE的數量關系,并證明.
【答案】(1)證明見解析(2)AF=2CE+![]() BE
BE
【解析】
(1)連接OC,OE, 可得OC=OE=OA=OB=![]() AB,即點E在以O為圓心,OA為半徑的圓上,
AB,即點E在以O為圓心,OA為半徑的圓上,
即點E在△ABC的外接圓⊙O上.
(2) 過點C作CG⊥CE,與BF交于點G,可證的∠BCG=∠ECA及△ACE≌△BCG(ASA),可得BG=AE,EC=GC,由旋轉的性質可得∠EFA=90°-∠EAF=45°=∠EAF,AE=EF,可得AF=2CE+![]() BE.
BE.
(1)①線段AB的中點;
②證明:如圖, 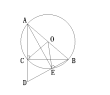
連接OC,OE,
∵AE⊥BD,
∴∠AEB=90°,
∵∠ACB=90°,O為AB中點,
∴OC=OE=OA=OB=![]() AB,
AB,
∴點E在以O為圓心,OA為半徑的圓上,
即點E在△ABC的外接圓⊙O上.
(2)①如上圖中所示, 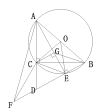
②AF=2CE+![]() BE;
BE;
證明如下:
過點C作CG⊥CE,與BF交于點G.
∴∠ECG=∠BCA=90°,
∴∠ECG+∠BCE=∠BCA+∠BCE,
即∠BCG=∠ECA.
∵E,A,B,C在以O為圓心,OA為半徑的圓上,
∴∠EAC=∠EBC.
∵BC=AC,
∴△ACE≌△BCG(ASA)
∴BG=AE,EC=GC.
∴在Rt△CEG中,EG=![]() .
.
∵由旋轉,∠EAF=45°,而∠AEF=90°,
∴∠EFA=90°-∠EAF=45°=∠EAF,
∴AE=EF,
∴在Rt△AEF中,AF=![]() .
.
∵BG=BE+EG=BE+![]() CE,
CE,
∴AF=2CE+![]() BE.
BE.


科目:初中數學 來源: 題型:
【題目】如圖,點P是⊙O 外一點,PA切⊙O于點A,AB是⊙O的直徑,連接OP,過點B作BC∥OP交⊙O于點C,連接AC交OP于點D.
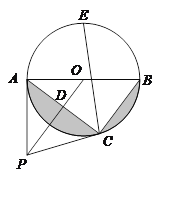
(1)求證:PC是⊙O的切線;
(2)若PD=![]() cm,AC=8cm,求圖中陰影部分的面積;
cm,AC=8cm,求圖中陰影部分的面積;
(3)在(2)的條件下,若點E是![]() 的中點,連接CE,求CE的長.
的中點,連接CE,求CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,AB=4cm,動點E從點A出發,以1cm/秒的速度沿折線AB—BC的路徑運動,到點C停止運動.過點E作 EF∥BD,EF與邊AD(或邊CD)交于點F,EF的長度y(cm)與點E的運動時間x(秒)的函數圖象大致是

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
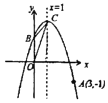
【題目】如圖,拋物線![]() 的頂點為
的頂點為![]() ,對稱軸為直線
,對稱軸為直線![]() ,且經過點
,且經過點![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
(1)求拋物線的解析式;
(2)連結![]() 、
、![]() ,求
,求![]() 的面積;
的面積;
(3)點![]() 是拋物線對稱軸上一點,若
是拋物線對稱軸上一點,若![]() 為等腰三角形,請直接寫出所有點
為等腰三角形,請直接寫出所有點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,園林小組的同學用一段長![]() 米的籬笆圍成一個一邊靠墻的矩形菜園
米的籬笆圍成一個一邊靠墻的矩形菜園![]() 墻的長為
墻的長為![]() 米,設
米,設![]() 的長為
的長為![]() 米,
米,![]() 的長為
的長為![]() 米.
米.
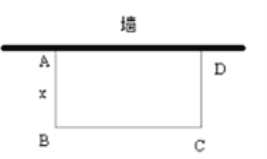
(1)①寫出![]() 與
與![]() 的函數關系是:
的函數關系是:
②自變量![]() 的取值范圍是
的取值范圍是
(2)園林小組的同學計劃使矩形菜園的面積為![]() 平方米,試求此時邊
平方米,試求此時邊![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著社會經濟的發展,汽車逐漸走入平常百姓家.某數學興趣小組隨機抽取了我市某單位部分職工進行調查,對職工購車情況分4類(A:車價40萬元以上;B:車價在20﹣40萬元;C:車價在20萬元以下;D:暫時未購車)進行了統計,并將統計結果繪制成以下條形統計圖和扇形統計圖.請結合圖中信息解答下列問題:

(1)調查樣本人數為 ,樣本中B類人數百分比是 ,其所在扇形統計圖中的圓心角度數是 ;
(2)把條形統計圖補充完整;
(3)該單位甲、乙兩個科室中未購車人數分別為2人和3人,現從這5個人中選2人去參觀車展,用列表或畫樹狀圖的方法,求選出的2人來自不同科室的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校舉行圖書節義賣活動,將所售款項捐給其他貧困學生.在這次義賣活動中,某班級售書情況如下圖:
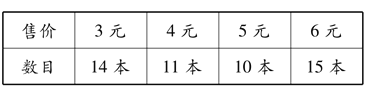
下列說法正確的是( )
A.該班級所售圖書的總數收入是226元
B.在該班級所售圖書價格組成的一組數據中,中位數是4
C.在該班級所售圖書價格組成的一組數據中,眾數是15
D.在該班級所售圖書價格組成的一組數據中,方差是2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國家近年來實施了新一輪農村電網改造升級工程,解決了農村供電“最后1公里”問題,電力公司在改造時把某一輸電線鐵塔建在了一個坡度為1:0.75的山坡CD的平臺BC上(如圖),測得∠AED=52°,BC=5米,CD=35米,DE=19米,則鐵塔AB的高度約為(參考數據:sin52°≈0.79,tan52°≈1.28)( )

A.28米B.29.6米C.36.6米D.57.6米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com