
【題目】已知:直線![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別是直線
分別是直線![]() ,
,![]() 上任意兩點(diǎn),在直線
上任意兩點(diǎn),在直線![]() 上取一點(diǎn)
上取一點(diǎn)![]() ,使
,使![]() ,連接
,連接![]() ,在直線
,在直線![]() 上任取一點(diǎn)
上任取一點(diǎn)![]() ,作
,作![]() ,
,![]() 交直線
交直線![]() 于點(diǎn)
于點(diǎn)![]() .
.
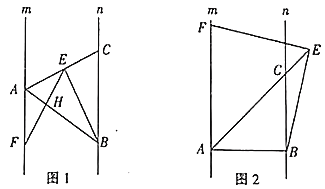
(1)如圖1,若點(diǎn)![]() 是線段
是線段![]() 上任意一點(diǎn),
上任意一點(diǎn),![]() 交
交![]() 于
于![]() ,求證:
,求證:![]() ;
;
(2)如圖2,點(diǎn)![]() 在線段
在線段![]() 的延長線上時(shí),
的延長線上時(shí),![]() 與
與![]() 互為補(bǔ)角,若
互為補(bǔ)角,若![]() ,請判斷線段
,請判斷線段![]() 與
與![]() 的數(shù)量關(guān)系,并說明理由.
的數(shù)量關(guān)系,并說明理由.
【答案】(1)見解析;(2)![]() ,見解析
,見解析
【解析】
(1)以點(diǎn)E為圓心,以EA為半徑畫弧交直線m于點(diǎn)M,連接EM,證明△AEB≌△MEF,根據(jù)全等三角形的性質(zhì)證明;
(2)在直線m上截取AN=AB,連接NE,證明△NAE≌△ABE,根據(jù)全等三角形的性質(zhì)得到EN=EB,∠ANE=∠ABE,證明EN=EF,等量代換即可.
(1)如圖1,
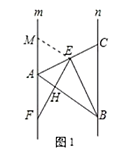
以點(diǎn)E為圓心,以EA為半徑畫弧交直線m于點(diǎn)M,連接EM,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)![]() .
.
理由如下:如圖2,
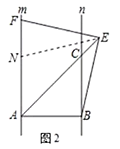
在直線![]() 上截取
上截取![]() ,連接
,連接![]() ,
,
∵![]() ,AB=BC,
,AB=BC,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,
,![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .下列說法錯(cuò)誤的是( ).
.下列說法錯(cuò)誤的是( ).
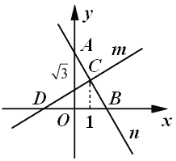
A.![]() B.
B.![]()
C.![]() D.直線
D.直線![]() 的函數(shù)表達(dá)式為
的函數(shù)表達(dá)式為![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某文具店計(jì)劃購進(jìn)![]() ,
,![]() 兩種筆記本共60本,每本
兩種筆記本共60本,每本![]() 種筆記本比
種筆記本比![]() 種筆記本的利潤高3元,銷售2本
種筆記本的利潤高3元,銷售2本![]() 種筆記本與3本
種筆記本與3本![]() 種筆記本所得利潤相同,其中
種筆記本所得利潤相同,其中![]() 種筆記本的進(jìn)貨量不超過進(jìn)貨總量的
種筆記本的進(jìn)貨量不超過進(jìn)貨總量的![]() ,
,![]() 種筆記本的進(jìn)貨量不少于30本.
種筆記本的進(jìn)貨量不少于30本.
(1)每本![]() 種筆記本與
種筆記本與![]() 種筆記本的利潤各為多少元?
種筆記本的利潤各為多少元?
(2)設(shè)購進(jìn)![]() 種筆記本
種筆記本![]() 本,銷售總利潤為
本,銷售總利潤為![]() 元,文具店應(yīng)如何安排進(jìn)貨才能使得
元,文具店應(yīng)如何安排進(jìn)貨才能使得![]() 最大?
最大?
(3)實(shí)際進(jìn)貨時(shí),![]() 種筆記本進(jìn)價(jià)下降
種筆記本進(jìn)價(jià)下降![]() (
(![]() )元.若兩種筆記本售價(jià)不變,請?jiān)O(shè)計(jì)出筆記本銷售總利潤最大的進(jìn)貨方案.
)元.若兩種筆記本售價(jià)不變,請?jiān)O(shè)計(jì)出筆記本銷售總利潤最大的進(jìn)貨方案.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(2011內(nèi)蒙古赤峰,7,3分)早晨,小張去公園晨練,下圖是他離家的距離y(千
米)與時(shí)間t(分鐘)的函數(shù)圖象,根據(jù)圖象信息,下列說法正確的是 ( )

A.小張去時(shí)所用的時(shí)間多于回家所用的時(shí)間B.小張?jiān)诠珗@鍛煉了20分鐘
C.小張去時(shí)的速度大于回家的速度 D.小張去時(shí)走上坡路,回家時(shí)走下坡路
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
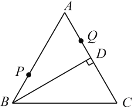
【題目】如圖,等邊△![]() 中,
中,![]() 于
于![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 、
、![]() 分別為
分別為![]() 、
、![]() 上的兩個(gè)定點(diǎn)且
上的兩個(gè)定點(diǎn)且![]() ,在
,在![]() 上有一動點(diǎn)
上有一動點(diǎn)![]() 使
使![]() 最短,則
最短,則![]() 的最小值為_____
的最小值為_____![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
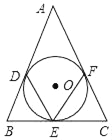
【題目】如圖,△ABC的三邊分別切⊙O于D,E,F(xiàn).
(1)若∠A=40°,求∠DEF的度數(shù);
(2)AB=AC=13,BC=10,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
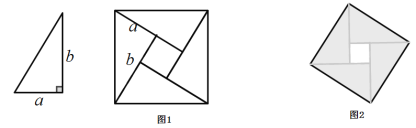
【題目】我國古代數(shù)學(xué)家趙爽曾用圖1證明了勾股定理,這個(gè)圖形被稱為“弦圖”.2002年在北京召開的國際數(shù)學(xué)家大會(ICM 2002)的會標(biāo)(圖2),其圖案正是由“弦圖”演變而來.“弦圖”是由4個(gè)全等的直角三角形與一個(gè)小正方形組成,恰好拼成一個(gè)大正方形請你根據(jù)圖1解答下列問題:
(1)敘述勾股定理(用文字及符號語言敘述);
(2)證明勾股定理;
(3)若大正方形的面積是![]() ,小正方形的面積是
,小正方形的面積是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
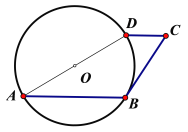
【題目】如圖,⊙O的直徑AD長為6,AB是弦,CD∥AB,∠A=30°,且CD=![]() .
.
(1)求∠C的度數(shù);
(2)求證:BC是⊙O的切線.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點(diǎn)D在邊BC上,連接AD .
(1)試?yán)贸咭?guī)作圖,求作:線段AE,使得AE是線段AD繞點(diǎn)A沿逆時(shí)針方向旋轉(zhuǎn)得到的,且![]() (保留作圖痕跡,不寫作法于證明過程);
(保留作圖痕跡,不寫作法于證明過程);
(2)連接DE交AC于F,若![]() ,求
,求![]() 的度數(shù).
的度數(shù).

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com