
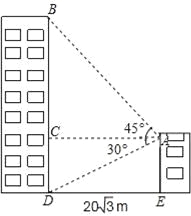
【題目】小敏家對面新建了一幢圖書大廈,小敏在自家窗口測得大廈頂部的仰角為45°,大廈底部的仰角為30°,如圖所示,量得兩幢樓之間的距離為20![]() 米.
米.
(1)求出大廈的高度BD;
(2)求出小敏家的高度AE.
【答案】(1)大廈的高度BD為:(20![]() +20)米;
+20)米;
(2)小敏家的高度AE為20米.
【解析】試題分析:(1)易得四邊形AEDC是矩形,即可求得AC的長,然后分別在Rt△ABC與Rt△ACD中,利用三角函數的知識求得BC與CD的長,繼而求得答案;
(2)結合(1),由四邊形AEDC是矩形,即可求得小敏家的高度AE.
試題解析:(1)如圖,∵AC⊥BD,
∴BD⊥DE,AE⊥DE,
∴四邊形AEDC是矩形,
∴AC=DE=20![]() 米,
米,
∵在Rt△ABC中,∠BAC=45°,
∴BC=AC=20![]() 米,
米,
在Rt△ACD中,tan30°=![]() ,
,
∴CD=ACtan30°=20![]() ×
×![]() =20(米),
=20(米),
∴BD=BC+CD=20![]() +20(米);
+20(米);
∴大廈的高度BD為:(20![]() +20)米;
+20)米;
(2)∵四邊形AEDC是矩形,
∴AE=CD=20米.
∴小敏家的高度AE為20米.


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 的解析表達式為:y=-3x+3,且
的解析表達式為:y=-3x+3,且![]() 與x軸交于點D,直線
與x軸交于點D,直線![]() 經過點A,B,直線
經過點A,B,直線![]() ,
,![]() 交于點C.
交于點C.
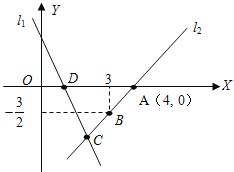
(1)求點D的坐標;
(2)求直線![]() 的解析表達式;
的解析表達式;
(3)求△ADC的面積;
(4)在直線![]() 上存在異于點C的另一點P,使得△ADP的面積是△ADC面積的2倍,請直接寫出點P的坐標.
上存在異于點C的另一點P,使得△ADP的面積是△ADC面積的2倍,請直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
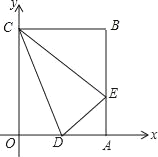
【題目】矩形OABC在平面直角坐標系中的位置如圖所示,點B的坐標為(3,4),D是OA的中點,點E在AB上,當△CDE的周長最小時,點E的坐標為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D是BC邊上的一點,∠B=50°,∠BAD=30°,將△ABD沿AD折疊得到△AED,AE與BC交于點F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
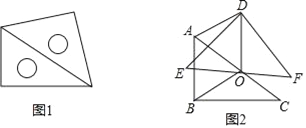
【題目】如圖1,放置的一副三角尺,將含45°角的三角尺斜邊中點O為旋轉中心,逆時針旋轉30°得到如圖2,連接OB、OD、AD.
(1)求證:△AOB≌△AOD;
(2)試判定四邊形ABOD是什么四邊形,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是根據九年級某班50名同學一周的鍛煉情況繪制的條形統計圖,下面關于該班50名同學一周鍛煉時間的說法錯誤的是( )
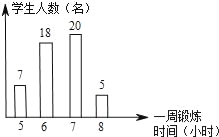
A. 平均數是6.5
B. 中位數是6.5
C. 眾數是7
D. 平均每周鍛煉超過6小時的人占總數的一半
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,BC=2AB,對角線相交于O,過C點作CE⊥BD交BD于E點,H為BC中點,連接AH交BD于G點,交EC的延長線于F點,下列5個結論:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四邊形GHCE;⑤CF=BD.正確的有( )個.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,動點P在平面直角坐標系中按圖中箭頭所示方向運動,第1次從原點運動到點(1,1),第2次接著運動到點(2,0),第3次接著運動到點(3,2),……,按這樣的運動規律,經過第2018次運動后,動點P的坐標是( )

A. (2018,1)B. (2018,0)C. (2018,2)D. (2017,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)已知二次函數![]() .
.
(1)如果二次函數的圖象與x軸有兩個交點,求m的取值范圍;
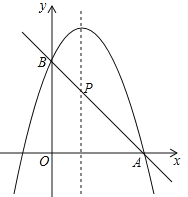
(2)如圖,二次函數的圖象過點A(3,0),與y軸交于點B,直線AB與這個二次函數圖象的對稱軸交于點P,求點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com