
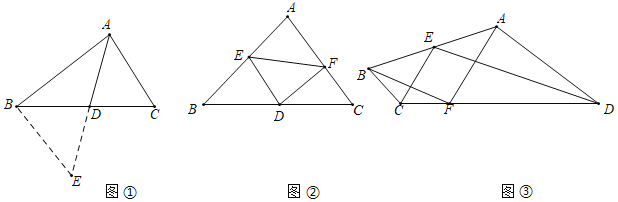
【題目】在利用構造全等三角形來解決的問題中,有一種典型的利用倍延中線的方法,例如:在△ABC中,AB=8,AC=6,點D是BC邊上的中點,怎樣求AD的取值范圍呢?我們可以延長AD到點E,使AD=DE,然后連接BE(如圖①),這樣,在△ADC和△EDB中,由于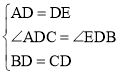 ,∴△ADC≌△EDB,∴AC=EB,接下來,在△ABE中通過AE的長可求出AD的取值范圍.
,∴△ADC≌△EDB,∴AC=EB,接下來,在△ABE中通過AE的長可求出AD的取值范圍.
請你回答:
(1)在圖①中,中線AD的取值范圍是 .
(2)應用上述方法,解決下面問題
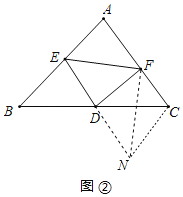
①如圖②,在△ABC中,點D是BC邊上的中點,點E是AB邊上的一點,作DF⊥DE交AC邊于點F,連接EF,若BE=4,CF=2,請直接寫出EF的取值范圍.
②如圖③,在四邊形ABCD中,∠BCD=150°,∠ADC=30°,點E是AB中點,點F在DC上,且滿足BC=CF,DF=AD,連接CE、ED,請判斷CE與ED的位置關系,并證明你的結論.
【答案】(1)1<AD<7;(2)①2<EF<6;②CE⊥ED,理由見解析
【解析】
(1)在△ABE中,根據三角形的三邊關系定理即可得出結果;
(2)①延長ED到點N,使![]() ,連接CN、FN,由SAS證得
,連接CN、FN,由SAS證得![]() ,得出
,得出![]() ,由等腰三角形的性質得出
,由等腰三角形的性質得出![]() ,在△CFN中,根據三角形的三邊關系定理即可得出結果;
,在△CFN中,根據三角形的三邊關系定理即可得出結果;
②延長CE與DA的延長線交于點G,易證DG∥BC,得出![]() ,由ASA證得
,由ASA證得![]() ,得出
,得出![]() ,即可證得
,即可證得![]() ,由
,由![]() ,根據等腰三角形的性質可得出
,根據等腰三角形的性質可得出![]() .
.
(1)在△ABE中,由三角形的三邊關系定理得:![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
故答案為:![]() ;
;
(2)①如圖②,延長ED到點N,使![]() ,連接CN、FN
,連接CN、FN
∵點D是BC邊上的中點
![]()
在△NDC和△EDB中,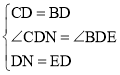
![]()
![]()
![]()
![]() 是等腰三角形,
是等腰三角形,![]()
在△CFN中,由三角形的三邊關系定理得:![]()
![]() ,即
,即![]()
![]() ;
;
②![]() ;理由如下:
;理由如下:
如圖③,延長CE與DA的延長線交于點G
∵點E是AB中點
![]()
![]()
![]()
![]()
在△GAE和△CBE中,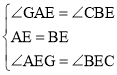
![]()
![]()
![]()
![]() ,即
,即![]()
![]()
![]() .(等腰三角形的三線合一)
.(等腰三角形的三線合一)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
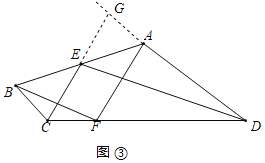
【題目】如圖,已知△ABC是等邊三角形, D、 E分別在邊AB、AC上,且AD=CE,CD與BE相交于點O.
(1)如圖①,求∠BOD的度數;
(2)如圖②,如果點D、 E分別在邊AB、CA的延長線上時,且AD=CE,求∠BOD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以點P(-1,0)為圓心的圓,交x軸于B、C兩點(B在C的左側),交y軸于A、D兩點(A在D的下方),AD=![]() ,將△ABC繞點P旋轉180°,得到△MCB.
,將△ABC繞點P旋轉180°,得到△MCB.

(1)求B、C兩點的坐標;
(2)請在圖中畫出線段MB、MC,并判斷四邊形ACMB的形狀(不必證明),求出點M的坐標;
(3)動直線l從與BM重合的位置開始繞點B順時針旋轉,到與BC重合時停止,設直線l與CM交點為E,點Q為BE的中點,過點E作EG⊥BC于G,連接MQ、QG.請問在旋轉過程中∠MQG的大小是否變化?若不變,求出∠MQG的度數;若變化,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,將AB邊沿AD折疊,發現B點的對應點E正好在AC的垂直平分線上,則∠C=_______
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司試銷一種成本單價為50元/件的新產品,規定試銷時銷售單價不低于成本單價,又不高于80元/件,經試銷調查,發現銷售量y(件)與銷售單價x(元/件)可近似看作一次函數y=kx+b的關系(如圖所示)
(I)根據圖象,求一次函數y=kx+b的解析式,并寫出自變量x的取值范圍;
(Ⅱ)該公司要想每天獲得最大的利潤,應把銷售單價定為多少?最大利潤值為多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
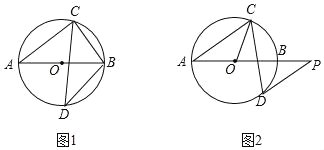
【題目】已知AB是⊙O的直徑,弦CD與AB相交,∠BAC=40°.
(1)如圖1,若D為弧AB的中點,求∠ABC和∠ABD的度數;
(2)如圖2,過點D作⊙O的切線,與AB的延長線交于點P,若DP∥AC,求∠OCD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
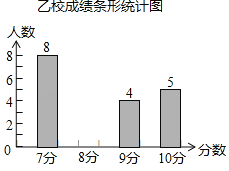
【題目】甲、乙兩校參加學生英語口語比賽,兩校參賽人數相等.比賽結束后,發現學生成績分別為7分、8分、9分、10分(滿分為10分),乙校平均分是8.3分,乙校的中位數是8分.依據統計數據繪制了如下尚不完整的甲校成績統計表和乙校成績統計圖;
甲校成績統計表
分數 | 7分 | 8分 | 9分 | 10分 |
人數 | 11 | 0 | ■ | 8 |
(1)請你將乙校成績統計圖直接補充完整;
(2)請直接寫出甲校的平均分是 ,甲校的中位數是 ,甲校的眾數是 ,從平均分和中位數的角度分析 校成績較好(填“甲”或“乙”).
查看答案和解析>>
科目:初中數學 來源: 題型:
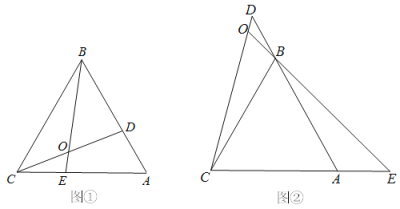
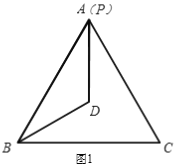
【題目】已知△ABC是等邊三角形,P為△ABC所在平面內一個動點,BP=BA,若0°﹤∠PBC﹤ 180°,且∠PBC的平分線上一點D滿足DB=DA.
(1)當BP和BA重合時(如圖1),則∠BPD=______°.
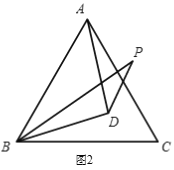
(2)當BP在∠ABC內部時(如圖2),求∠BPD的度數
(3)當BP在∠ABC外部時,請直接寫出∠BPD的度數,并畫出相應的圖形.
查看答案和解析>>
科目:初中數學 來源: 題型:
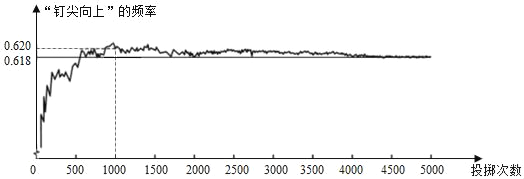
【題目】如圖顯示了用計算機模擬隨機投擲一枚圖釘的某次實驗的結果.下面有三個推斷:①某次實驗投擲次數是500,計算機記錄“釘尖向上”的次數是308,則該次試驗“釘尖向上”的頻率是0.616;②隨著實驗次數的增加,“釘尖向上”的頻率總在0.618附近擺動,顯示出一定的穩定性,可以估計“釘尖向上”的概率是0.618;③若再次用計算機模擬實驗,則當投擲次數為1000時,“釘尖向上”的概率一定是0.620.其中合理的是( )
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com