
【題目】小李去買套裝![]() 色水筆和筆記本,若購買
色水筆和筆記本,若購買![]() 袋筆和
袋筆和![]() 本筆記本,他身上的錢還差
本筆記本,他身上的錢還差![]() 元,若改 成購買
元,若改 成購買![]() 袋筆和
袋筆和![]() 本筆記本,他身上的錢會剩下
本筆記本,他身上的錢會剩下![]() 元.若他把身上的錢都花掉,購買這兩種 物品(兩種都買)的方案有( )
元.若他把身上的錢都花掉,購買這兩種 物品(兩種都買)的方案有( )
A.![]() 種B.
種B.![]() 種C.
種C.![]() 種D.
種D.![]() 種
種
【答案】C
【解析】
設1袋筆的價格為x元,1本筆記本的價格為y元,根據“若購買4袋筆和6本筆記本,他身上的錢還差22元,若改成購買1袋筆和2本筆記本,他身上的錢會剩下34元”,即可得出關于x,y的二元一次方程,結合x,y均為正整數即可得出結論,再設可購買a袋筆和b本筆記本,根據總價=單價×數量可得出關于a,b的二元一次方程,結合a,b均為正整數即可得出結論.
設1袋筆的價格為x元,1本筆記本的價格為y元,
依題意,得:4x+6y-22=x+2y+34,
∴3x+4y=56,即y=14-![]() x.
x.
∵x,y均為正整數,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
設可購買a袋筆和b本筆記本.
①當x=4,y=11時,4x+6y-22=60,
∴4a+11b=60,即a=15-![]() b,
b,
∵a,b均為正整數,
∴![]() ;
;
②當x=8,y=8時,4x+6y-22=58,
∴8a+8b=58,即a+b=![]() ,
,
∵a,b均為正整數,
∴方程無解;
③當x=12,y=5時,4x+6y-22=56,
∴12a+5b=56,即b=![]() ,
,
∵a,b均為正整數,
∴![]() ;
;
④當x=16,y=2時,4x+6y-22=54,
∴16a+2b=54,即b=27-8a,
∵a,b均為正整數,
∴![]() ,
,![]() ,
,![]() .
.
綜上所述,共有5種購進方案.
故選:C.


科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,∠B=90°,
中,∠B=90°,![]() ,點D,E分別是邊BC,AC的中點,連接
,點D,E分別是邊BC,AC的中點,連接![]() 將
將![]() 繞點C按順時針方向旋轉,記旋轉角為
繞點C按順時針方向旋轉,記旋轉角為![]() .
.
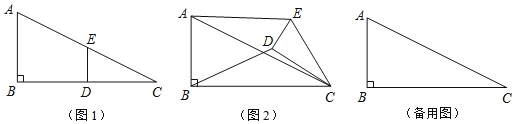
![]() 問題發現:
問題發現:
![]() 當
當![]() 時,
時,![]() _____;
_____;![]() 當
當![]() 時,
時,![]() _____.
_____.
![]() 拓展探究:
拓展探究:
試判斷:當![]() 時,
時,![]() 的大小有無變化?請僅就圖2的情況給出證明.
的大小有無變化?請僅就圖2的情況給出證明.
![]() 問題解決:
問題解決:
當![]() 旋轉至A、D、E三點共線時,直接寫出線段BD的長.
旋轉至A、D、E三點共線時,直接寫出線段BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
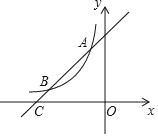
【題目】如圖,一次函數y=x+4的圖象與反比例函數y=![]() (k為常數且k≠0)的圖象交于A(﹣1,a),B兩點,與x軸交于點C.
(k為常數且k≠0)的圖象交于A(﹣1,a),B兩點,與x軸交于點C.
(1)求a,k的值及點B的坐標;
(2)若點P在x軸上,且S△ACP=![]() S△BOC,直接寫出點P的坐標.
S△BOC,直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
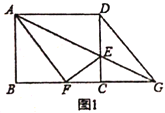
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 邊上一點,連接
邊上一點,連接![]() ,將矩形
,將矩形![]() 沿
沿![]() 折疊,頂點
折疊,頂點![]() 恰好落在
恰好落在![]() 邊上點
邊上點![]() 處,延長
處,延長![]() 交
交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() .
.
(1)求![]() 的值;
的值;
(2)求證:四邊形![]() 是菱形;
是菱形;
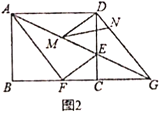
(3)如圖2,![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 上的動點(與端點不重合),且
上的動點(與端點不重合),且![]() ,設
,設![]() ,
,![]() ,請解決以下相關問題:
,請解決以下相關問題:
①寫出![]() 關于
關于![]() 的函數解析式;
的函數解析式;
②是否存在這樣的點![]() ,使
,使![]() 是等腰三角形?若存在,請求出
是等腰三角形?若存在,請求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校數學課外實踐小組一次活動中,測量一座樓房的高度.如圖,在山坡坡腳A處測得這座樓房的樓頂B點的仰角為60°,沿山坡往上走到C處再測得B點的仰角為45°,已知山坡的坡比i=1:![]() ,OA=200m,且O、A、D在同一條直線上.
,OA=200m,且O、A、D在同一條直線上.
(1)求樓房OB的高度;
(2)求山坡上AC的距離(結果保留根號)
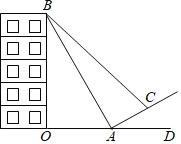
查看答案和解析>>
科目:初中數學 來源: 題型:
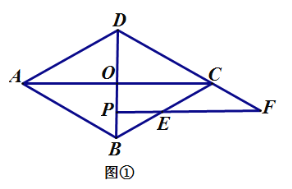
【題目】已知菱形![]() 的對角線交于點
的對角線交于點![]() 是直線
是直線![]() 上任意一點(異于點
上任意一點(異于點![]() ),過點
),過點![]() 作平行于
作平行于![]() 的直線交直線
的直線交直線![]() 于點
于點![]() ,交直線
,交直線![]() 于點
于點![]() .
.
(1)當點![]() 在線段
在線段![]() 上時,如圖 ①,易證:
上時,如圖 ①,易證:![]() (不用證明);
(不用證明);
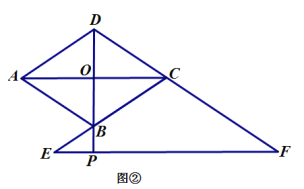
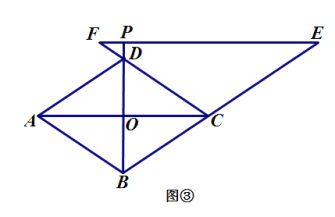
(2)當點![]() 在線段
在線段![]() 的延長線上時,如圖 ②;當點
的延長線上時,如圖 ②;當點![]() 在線段
在線段![]() 的延長線上時,如圖 ③,線段
的延長線上時,如圖 ③,線段![]() 之間又有怎樣的數量關系? 請寫出你的猜想,并選擇其中一種情況加以證明.
之間又有怎樣的數量關系? 請寫出你的猜想,并選擇其中一種情況加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為更新果樹品種,某果園計劃新購進![]() 、
、![]() 兩個品種的果樹苗栽植培育,若計劃購進這兩種果樹苗共45棵,其中
兩個品種的果樹苗栽植培育,若計劃購進這兩種果樹苗共45棵,其中![]() 種苗的單價為
種苗的單價為![]() 元/棵,購買
元/棵,購買![]() 種苗所需費用
種苗所需費用![]() (元)與購買數量
(元)與購買數量![]() (棵)之間存在如圖所示的函數關系.
(棵)之間存在如圖所示的函數關系.
(1)求![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)若在購買計劃中,![]() 種苗的數量不超過35棵,但不少于
種苗的數量不超過35棵,但不少于![]() 種苗的數量,請設計購買方案,使總費用最低,并求出最低費用.
種苗的數量,請設計購買方案,使總費用最低,并求出最低費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
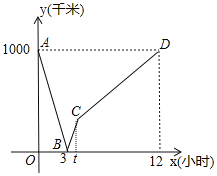
【題目】一列動車從甲地開往乙地, 一列普通列車從乙地開往甲地,兩車均勻速行駛并同時出發,設普通列車行駛的時間為![]() (小時),兩車之間的距離為
(小時),兩車之間的距離為![]() (千米),如圖中的折線表示
(千米),如圖中的折線表示![]() 與
與![]() 之間的函數關系,下列說法:①動車的速度是
之間的函數關系,下列說法:①動車的速度是![]() 千米/小時;②點B的實際意義是兩車出發后
千米/小時;②點B的實際意義是兩車出發后![]() 小時相遇;③甲、乙兩地相距
小時相遇;③甲、乙兩地相距![]() 千米;④普通列車從乙地到達甲地時間是
千米;④普通列車從乙地到達甲地時間是![]() 小時,其中不正確的有( )
小時,其中不正確的有( )
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 經過點
經過點![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 是拋物線上一個動點,設點
是拋物線上一個動點,設點![]() 的橫坐標為
的橫坐標為![]() .連接
.連接![]() ,
,![]() ,
,![]() ,
,![]() .
.
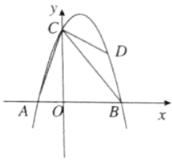
(1)求拋物線的函數表達式;
(2)![]() 的面積何時最大?求出此時
的面積何時最大?求出此時![]() 點的坐標和最大面積;
點的坐標和最大面積;
(3)在(2)的條件下,若點![]() 是
是![]() 軸上一動點,點
軸上一動點,點![]() 是拋物線上一動點,試判斷是否存在這樣的點
是拋物線上一動點,試判斷是否存在這樣的點![]() ,使得以點
,使得以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是平行四邊形?若存在,請直接寫出點
為頂點的四邊形是平行四邊形?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com