
【題目】書店舉行購書優惠活動:
①一次性購書不超過100元,不享受打折優惠;
②一次性購書超過100元但不超過200元,一律按原價打九折;
③一次性購書超過200元,一律按原價打七折.
小麗在這次活動中,兩次購書總共付款229.4元,第二次購書原價是第一次購書原價的3倍,那么小麗這兩次購書原價的總和是_________.
【答案】248元或296元
【解析】
設小麗第一次購書的原價為x元,則第二次購書的原價為3x元,分x≤![]() 、
、![]() <x≤
<x≤![]() 、
、![]() <x≤100及x>100四種情況,找出關于x的一元一次方程,解之即可得出結論.
<x≤100及x>100四種情況,找出關于x的一元一次方程,解之即可得出結論.
設小麗第一次購書的原價為x元,則第二次購書的原價為3x元,
根據題意得:當3x≤100,即x≤![]() 時,x+3x=229.4,
時,x+3x=229.4,
解得:x=57.35(舍去);
當100<3x≤200,即![]() <x≤
<x≤![]() 時,x+0.9×3x=229.4,
時,x+0.9×3x=229.4,
解得:x=62,
∴x+3x=248;
當3x>200且x≤100,即![]() <x≤100時,x+0.7×3x=229.4,
<x≤100時,x+0.7×3x=229.4,
解得:x=74,
∴x+3x=296;
當x>100時,0.9x+0.7×3x=229.4,
解得:x≈76.47(舍去).
答:小麗這兩次購書原價的總和是248元或296元.
故填:248元或296元.


科目:初中數學 來源: 題型:
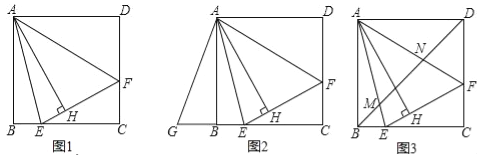
【題目】如圖1,在正方形ABCD內作∠EAF=45°,AE交BC于點E,AF交CD于點F,連接EF,過點A作AH⊥EF,垂足為H.
(1)如圖2,將△ADF繞點A順時針旋轉90°得到△ABG.
①求證:△AGE≌△AFE;
②若BE=2,DF=3,求AH的長.
(2)如圖3,連接BD交AE于點M,交AF于點N.請探究并猜想:線段BM,MN,ND之間有什么數量關系?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩根木條,一根長20cm,另一根長24cm,將它們一端重合且放在同一條直線上,此時兩根木條的中點之間的距離為( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
科目:初中數學 來源: 題型:
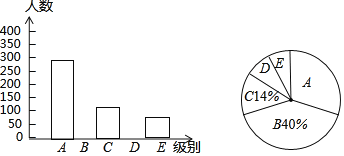
【題目】某報社為了了解市民“獲取新聞的最主要途徑”,開展了一次抽樣調查,根據調查結果繪制了如圖三種不完整的統計圖表.
組別 | 獲取新聞的最主要途徑 | 人數 |
A | 電腦上網 | 280 |
B | 手機上網 | m |
C | 電視 | 140 |
D | 報紙 | n |
E | 其它 | 80 |
請根據圖表信息解答下列問題:
(1)統計表中的m= ,n= ,并請補全條形統計圖;
(2)扇形統計圖中“D”所對應的圓心角的度數是 ;
(3)若該市約有120萬人,請你估計其中將“電腦上網”和“手機上網”作為“獲取新聞的最主要途徑”的總人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
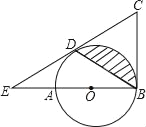
【題目】如圖,AB是⊙O的直徑,BC是⊙O的切線,D為⊙O上的一點,CD=CB,延長CD交BA的延長線于點E,
(1)求證:CD為⊙O的切線;
(2)若EA=BO=2,求圖中陰影部分的面積(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
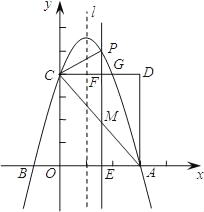
【題目】如圖,拋物線y=ax2﹣2ax+c(a≠0)交x軸于A、B兩點,A點坐標為(3,0),與y軸交于點C(0,4),以OC、OA為邊作矩形OADC交拋物線于點G.
(1)求拋物線的解析式;
(2)拋物線的對稱軸l在邊OA(不包括O、A兩點)上平行移動,分別交x軸于點E,交CD于點F,交AC于點M,交拋物線于點P,若點M的橫坐標為m,請用含m的代數式表示PM的長;
(3)在(2)的條件下,連結PC,則在CD上方的拋物線部分是否存在這樣的點P,使得以P、C、F為頂點的三角形和△AEM相似?若存在,求出此時m的值,并直接判斷△PCM的形狀;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C、D是線段AB上兩點,M、N分別是線段AD、BC的中點,下列結論:①若AD=BM,則AB=3BD;②若AC=BD,則AM=BN;③AC-BD=2(MC-DN);④2MN=AB-CD.其中正確的結論是( )
![]()
A.①②③B.③④C.①②④D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
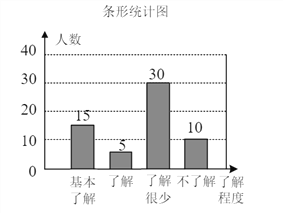
【題目】“食品安全”受到全社會的廣泛關注,濟南市某中學對部分學生就食品安全知識的了解程度,采用隨機抽樣調查的方式,并根據收集到的信息進行統計,繪制了下面兩份尚不完整的統計圖,請你根據統計圖中所提供的信息解答下列問題.
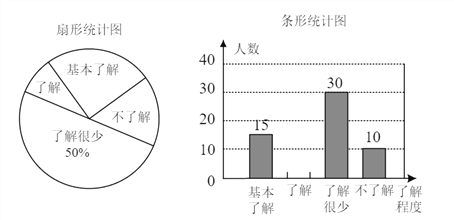
(1)接受問卷調查的學生共有_____人,扇形統計圖中“基本了解”部分所對應扇形的圓心角為_____.
(2)請補全條形統計圖.
(3)若該中學共有學生900人,請根據上述調查結果,估計該中學學生中對食品安全知識達到“了解”和“基本了解”程度的總人數.
(4)若從對食品安全知識達到“了解”程度的2個女生和2個男生中隨機抽取2人參加食品安全知識競賽,請用樹狀圖或列表法求出恰好抽到1個男生和1個女生的概率.
【答案】(1)60;90°;(2)補圖見解析;(3)300;(4)![]()
【解析】分析:(1)根據了解很少的人數除以了解很少的人數所占的百分百求出抽查的總人數,再用“基本了解”所占的百分比乘以360°,即可求出“基本了解”部分所對應扇形的圓心角的度數;(2)用調查的總人數減去“基本了解”“了解很少”和“基本了解”的人數,求出了解的人數,從而補全統計圖;(3)用總人數乘以“了解”和“基本了解”程度的人數所占的比例,即可求出達到“了解”和“基本了解”程度的總人數;(4)根據題意列出表格,再根據概率公式即可得出答案.
詳解:(1)60;90°.
(2)補全的條形統計圖如圖所示.
(3)對食品安全知識達到“了解”和“基本了解”的學生所占比例為![]() ,由樣本估計總體,該中學學生中對食品安全知識達到“了解”和“基本了解”程度的總人數為
,由樣本估計總體,該中學學生中對食品安全知識達到“了解”和“基本了解”程度的總人數為![]() .
.
(4)列表法如表所示,
男生 | 男生 | 女生 | 女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
女生 | 男生女生 | 男生女生 | 女生女生 | |
女生 | 男生女生 | 女生女生 |
所有等可能的情況一共12種,其中選中1個男生和1個女生的情況有8種,所以恰好選中1個男生和1個女生的概率是![]() .
.
點睛:本題考查了條形統計圖、扇形統計圖以及用列表法或樹狀圖法求概率,根據題意求出總人數是解題的關鍵;注意運用概率公式:概率=所求情況數與總情況數之比.
【題型】解答題
【結束】
24
【題目】為響應國家全民閱讀的號召,某社區鼓勵居民到社區閱覽室借閱讀書,并統計每年的借閱人數和圖書借閱總量(單位:本),該閱覽室在2015年圖書借閱總量是7500本,2017年圖書借閱總量是10800本.
(1)求該社區的圖書借閱總量從2015年至2017年的年平均增長率.
(2)已知2017年該社區居民借閱圖書人數有1350人,預計2018年達到1440人,如果2017年至2018年圖書借閱總量的增長率不低于2015年至2017年的年平均增長率,設2018年的人均借閱量比2017年增長a%,求a的值至少是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,正方形紙片ABCD的邊長為2,翻折∠B、∠D,使兩個直角的頂點重合于對角線BD上一點P、EF、GH分別是折痕(如圖2).設AE=x(0<x<2),給出下列判斷:①當x=1時,點P是正方形ABCD的中心;②當x=![]() 時,EF+GH>AC;③當0<x<2時,六邊形AEFCHG面積的最大值是3;④當0<x<2時,六邊形AEFCHG周長的值不變.其中正確的選項是( )
時,EF+GH>AC;③當0<x<2時,六邊形AEFCHG面積的最大值是3;④當0<x<2時,六邊形AEFCHG周長的值不變.其中正確的選項是( )
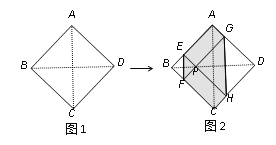
A. ①③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com