
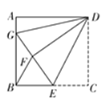
【題目】如圖,在正方形ABCD中,點E是BC邊的中點,將△DCE沿DE折疊,使點C落在點F處,延長EF交AB于點G,連接DG、BF.
(1)求證:DG平分∠ADF;
(2)若AB=12,求△EDG的面積.
【答案】(1)見解析;(2)60
【解析】
(1)由折疊可知,DF=DC=DA,∠DFE=∠C=90°,證明Rt△ADG≌Rt△FDG即可證明DG平分∠ADF;
(2)設AG=x,則BG=12-x,GE=x+6,在Rt△BEG中,根據勾股定理建立方程求出x,然后再求出面積即可.
解:(1)如圖,由折疊可知,DF=DC=DA,∠DFE=∠C=90°,
∴∠DFG=∠A=90°,
在Rt△ADG和Rt△FDG中,
![]()
∴Rt△ADG≌Rt△FDG(HL),
∴∠ADG=∠FDG,
∴DG平分∠ADF;
(2)∵AB=12,點E是BC邊的中點,
∴BE=CE=6,
∴EF=6,
設AG=x,
∴GF=x,BG=12-x,
∴GE=x+6,
在Rt△BEG中,
![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴GE=4+6=10,
∴S△EDG=10×12×![]() =60.
=60.


 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=3,BC=4,將對角線AC繞對角線交點O旋轉,分別交邊AD、BC于點E、F,點P是邊DC上的一個動點,且保持DP=AE,連接PE、PF,設AE=x(0<x<3).
(1)填空:PC= ,FC= ;(用含x的代數式表示)
(2)求△PEF面積的最小值;
(3)在運動過程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 是上半圓的弦,過點
是上半圓的弦,過點![]() 作
作![]() 的切線
的切線![]() 交
交![]() 的延長線于點
的延長線于點![]() ,過點
,過點![]() 作切線
作切線![]() 的垂線,垂足為
的垂線,垂足為![]() ,且與
,且與![]() 交于點
交于點![]() ,設
,設![]() ,
,![]() 的度數分別是
的度數分別是![]() .
.
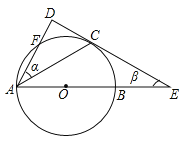
![]() 用含
用含![]() 的代數式表示
的代數式表示![]() ,并直接寫出
,并直接寫出![]() 的取值范圍;
的取值范圍;
![]() 連接
連接![]() 與
與![]() 交于點
交于點![]() ,當點
,當點![]() 是
是![]() 的中點時,求
的中點時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
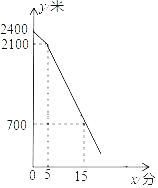
【題目】寒假中,小王向小李借一本數學培優資料,但相互找不到對方的家,電話中兩人商量,走兩家之間長度為2400米的一條路,相向而行.小李在小王出發5分鐘后帶上數學培優資料出發.在整個行走過程中,兩人均保持各自的速度勻速行走.兩人相距的路程y(單位:米)與小王出發的時間x(單位:分)之間的關系如圖所示,則兩人相遇時,小李走了_____米.
查看答案和解析>>
科目:初中數學 來源: 題型:
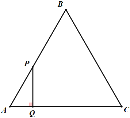
【題目】如圖,△ABC為等邊三角形,點P從點A出發沿A→B→C路徑勻速運動到點C,到達點C時停止運動,過點P作PQ⊥AC于點Q. 若△APQ的面積為y,AQ的長為x,則下列能反映y與x之間的大致圖象是 ( )
A. B.
B.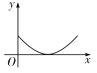 C.
C.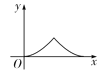 D.
D.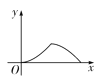
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,我們把橫、縱坐標都是整數的點叫做整點,已知點
中,我們把橫、縱坐標都是整數的點叫做整點,已知點![]() ,點
,點![]() 是
是![]() 軸正半軸上的點,記
軸正半軸上的點,記![]() 內部(不包括邊界)的整點個數為
內部(不包括邊界)的整點個數為![]() ,當
,當![]() 時,點
時,點![]() 的橫坐標
的橫坐標![]() 的取值范圍是____.
的取值范圍是____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“構造圖形解題”,它的應用十分廣泛,特別是有些技巧性很強的題目,如果不能發現題目中所隱含的幾何意義,而用通常的代數方法去思考,經常讓我們手足無措,難以下手,這時,如果能轉換思維,發現題目中隱含的幾何條件,通過構造適合的幾何圖形,將會得到事半功倍的效果,下面介紹兩則實例:
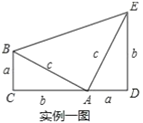
實例一:1876年,美國總統伽非爾德利用實例一圖證明了勾股定理:由![]() 四邊形
四邊形![]() 得
得![]() ,化簡得:
,化簡得:![]() .
.
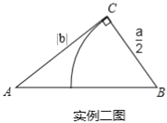
實例二:歐幾里得的《幾何原本》記載,關于![]() 的方程
的方程![]() 的圖解法是:畫
的圖解法是:畫![]() ,使
,使![]() ,
,![]() ,
,![]() ,再在斜邊
,再在斜邊![]() 上截取
上截取![]() ,則
,則![]() 的長就是該方程的一個正根(如實例二圖).
的長就是該方程的一個正根(如實例二圖).
根據以上閱讀材料回答下面的問題:
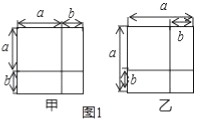
(1)如圖1,請利用圖形中面積的等量關系,寫出甲圖要證明的數學公式是 ,乙圖要證明的數學公式是 ,體現的數學思想是 ;
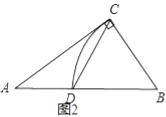
(2)如圖2,按照實例二的方式構造![]() ,連接
,連接![]() ,請用含字母
,請用含字母![]() 、
、![]() 的代數式表示
的代數式表示![]() 的長,
的長,![]() 的表達式能和已學的什么知識相聯系;
的表達式能和已學的什么知識相聯系;
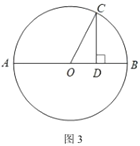
(3)如圖3,已知![]() ,
,![]() 為直徑,點
為直徑,點![]() 為圓上一點,過點
為圓上一點,過點![]() 作
作![]() 于點
于點![]() ,連接
,連接![]() ,設
,設![]() ,
,![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+2ax+c(a<0)的圖象與x軸交于A、B兩點,與y軸交于C點,頂點為D,一次函數y=mx﹣3的圖象與y軸交于E點,與二次函數的對稱軸交于F點,且tan∠FDC=![]() .
.
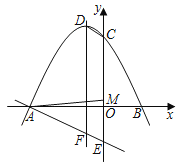
(1)求a的值;
(2)若四邊形DCEF為平行四邊形,求二次函數表達式.
(3)在(2)的條件下設點M是線段OC上一點,連接AM,點P從點A出發,先以1個單位長度/s的速度沿線段AM到達點M,再以![]() 個單位長度/s的速度沿MC到達點C,求點P到達點C所用最短時間為 s(直接寫出答案).
個單位長度/s的速度沿MC到達點C,求點P到達點C所用最短時間為 s(直接寫出答案).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com