
已知二次函數 的圖象經過點(4,3),(3,0).
的圖象經過點(4,3),(3,0).
(1)求b、c的值;
(2)求出該二次函數圖象的頂點坐標和對稱軸,并在所給坐標系中畫出該函數的圖象;
(3)該函數的圖像經過怎樣的平移得到 的圖像?
的圖像?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
已知直線y=x+6交x軸于點A,交y軸于點C,經過A和原點O的拋物線y=ax2+bx(a<0)的頂點B在直線AC上.
(1)求拋物線的函數關系式;
(2)以B點為圓心,以AB為半徑作⊙B,將⊙B沿x軸翻折得到⊙D,試判斷直線AC與⊙D的位置關系,并說明理由;
(3)若E為⊙B優弧 上一動點,連結AE、OE,問在拋物線上是否存在一點M,使∠MOA︰∠AEO=2︰3,若存在,試求出點M的坐標;若不存在,試說明理由.
上一動點,連結AE、OE,問在拋物線上是否存在一點M,使∠MOA︰∠AEO=2︰3,若存在,試求出點M的坐標;若不存在,試說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
某商店將進價為每件80元的某種商品按每件100元出售,每天可售出100件.經過市場調查,發現這種商品每件每降低1元,其銷售量就可增加10件.
(1)設每件商品降低售價 元,則降價后每件利潤 元,每天可售出 件(用含
元,則降價后每件利潤 元,每天可售出 件(用含 的代數式表示);
的代數式表示);
(2)如果商店為了每天獲得利潤2160元,那么每件商品應降價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
拋物線 經過點A(4,0),B(2,2),連結OB,AB.
經過點A(4,0),B(2,2),連結OB,AB.
(1)求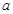 、
、 的值;
的值;
(2)求證:△OAB是等腰直角三角形;
(3)將△OAB繞點O按順時針方向旋轉l35°得到△OA′B′,寫出A′B′的中點P的出標.試判斷點P是否在此拋物線上,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平面直角坐標系中,已知拋物線 交
交 軸于A(2,0),B(6,0)兩點,交
軸于A(2,0),B(6,0)兩點,交 軸于點C(0,
軸于點C(0,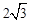 ).
).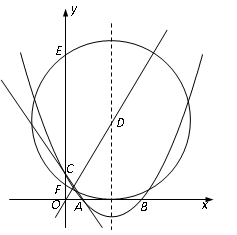
(1)求此拋物線的解析式;
(2)若此拋物線的對稱軸與直線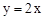 交于點D,作⊙D與x軸相切,⊙D交
交于點D,作⊙D與x軸相切,⊙D交 軸于點E、F兩點,求劣弧EF所對圓心角的度數;
軸于點E、F兩點,求劣弧EF所對圓心角的度數;
(3)P為此拋物線在第二象限圖像上的一點,PG垂直于 軸,垂足為點G,試確定P點的位置,使得△PGA的面積被直線AC分為1︰2兩部分.
軸,垂足為點G,試確定P點的位置,使得△PGA的面積被直線AC分為1︰2兩部分.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知拋物線y=ax2+bx+c(a≠0)的頂點坐標為(4,﹣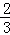 ),且與y軸交于點C(0,2),與x軸交于A,B兩點(點A在點B的左邊).
),且與y軸交于點C(0,2),與x軸交于A,B兩點(點A在點B的左邊).
(1)求拋物線的解析式及A,B兩點的坐標;
(2)在(1)中拋物線的對稱軸l上是否存在一點P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,請說明理由;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com