
【題目】如圖:反比例函數![]() 的圖象與一次函數
的圖象與一次函數![]() 的圖象交于
的圖象交于![]() 、
、![]() 兩點,其中
兩點,其中![]() 點坐標為
點坐標為![]() .
.

(1)求反比例函數與一次函數的表達式;
(2)觀察圖象,直接寫出當![]() 時,自變量
時,自變量![]() 的取值范圍;
的取值范圍;
(3)一次函數的圖象與![]() 軸交于點
軸交于點![]() ,點
,點![]() 是反比例函數圖象上的一個動點,若
是反比例函數圖象上的一個動點,若![]() ,求此時
,求此時![]() 點的坐標.
點的坐標.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)(12,
;(3)(12,![]() )或(-12,
)或(-12,![]() )
)
【解析】
(1)把A點坐標代入![]() 中求出k得到反比例函數解析式,把A點坐標代入
中求出k得到反比例函數解析式,把A點坐標代入![]() 中求出b得到一次函數解析式;
中求出b得到一次函數解析式;
(2)由函數圖象,寫出一次函數圖象在反比例函數圖象上方所對應的自變量的范圍即可;
(3)設P(x,![]() ),先利用一次解析式解析式確定C(0,1),再根據三角形面積公式得到
),先利用一次解析式解析式確定C(0,1),再根據三角形面積公式得到![]() ,然后解絕對值方程得到x的值,從而得到P點坐標.
,然后解絕對值方程得到x的值,從而得到P點坐標.
解:(1)把A(1,2)代入![]() 得k=2,
得k=2,
∴反比例函數解析式為![]() ,
,
把A(1,2)代入![]() 得
得![]() ,解得
,解得![]() ,
,
∴一次函數解析式為![]() ;
;
(2)由函數圖象可得:當y1<y2時,-2<x<0或x>1;
(3)設P(x,![]() ),
),
當x=0時,![]() ,
,
∴C(0,1),
∵S△OCP=6,
∴![]() ,解得
,解得![]() ,
,
∴P(12,![]() )或(-12,
)或(-12,![]() ).
).


科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD中,∠B=60°,AB=2cm,E、F分別是BC、CD的中點,連接AE、EF、AF,則△AEF的周長為( )

A.2![]() cmB.3
cmB.3![]() cmC.4
cmC.4![]() cmD.3cm
cmD.3cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,AC=BC,點D為AB中點.∠GDH=90°,∠GDH繞點D旋轉,DG,DH分別與邊AC,BC交于E,F兩點.下列結論:①AE+BF=![]() AB;②AE2+BF2=EF2;③S四邊形CEDF=
AB;②AE2+BF2=EF2;③S四邊形CEDF=![]() S△ABC;④△DEF始終為等腰直角三角形.其中正確的是( )
S△ABC;④△DEF始終為等腰直角三角形.其中正確的是( )

A.①②④B.①②③
C.①③④D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】撫順某中學為了解八年級學生的體能狀況,從八年級學生中隨機抽取部分學生進行體能測試,測試結果分為A,B,C,D四個等級.請根據兩幅統計圖中的信息回答下列問題:
(1)本次抽樣調查共抽取了多少名學生?
(2)求測試結果為C等級的學生數,并補全條形圖;
(3)若該中學八年級共有700名學生,請你估計該中學八年級學生中體能測試結果為D等級的學生有多少名?
(4)若從體能為A等級的2名男生2名女生中隨機的抽取2名學生,做為該校培養運動員的重點對象,請用列表法或畫樹狀圖的方法求所抽取的兩人恰好都是男生的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實驗數據顯示,一般成人喝半斤低度白酒后,1.5時內其血液中酒精含量y(毫克/百毫升)與時間x (時)的關系可近似地用二次函數y=-200x2+400x刻畫;1.5時后(包括1.5時)y與x可近似地用反比例函數![]() (k>0)刻畫(如圖所示).
(k>0)刻畫(如圖所示).
(1)根據上述數學模型計算:喝酒后幾時血液中的酒精含量達到最大值?最大值為多少
(2)按國家規定,車輛駕駛人員血液中的酒精含量大于或等于20毫克/百毫升時屬于“酒后駕駛”,不能駕車上路.參照上述數學模型,假設某駕駛員晚上20:30在家喝完半斤低度白酒,第二天早上7:00能否駕車去上班?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,點E、F、H分別是AB、BC、CD的中點,CE、DF交于G,連接AG、HG.下列結論:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG=![]() AD.其中正確的有( )
AD.其中正確的有( )
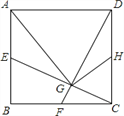
A. ① ② B. ① ② ④ C. ① ③ ④ D. ① ② ③ ④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某蔬菜公司收購蔬菜進行銷售的獲利情況如下表所示:
銷售方式 | 直接銷售 | 粗加工后銷售 | 精加工后銷售 |
每噸獲利/元 | 100 | 250 | 450 |
現在該公司收購了140噸蔬菜,已知該公司每天能精加工蔬菜6噸或粗加工蔬菜16噸(兩種加工不能同時進行)。
(1)如果要求在18天內全部銷售完這140噸蔬菜,請完成下列表格:
銷售方式 | 全部直接銷售 | 全部粗加工銷售 | 盡量精加工,剩 余部分直接銷售 |
獲利/元 |
(2)如果先進行精加工,然后進行粗加工,要求在15天內剛好加工完140噸蔬菜,則應如何分配加工時間?
(3)如果要求蔬菜都要加工后銷售,且公司獲利不能少于42200元,問:至少將多少噸蔬菜進行精加工?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小東設計的“過直線外一點作這條直線的平行線”的尺規作圖過程
已知:直線l及直線l外一點P.

求作:直線PQ,使得PQ∥l.
作法:如圖,

①在直線l上取一點A,作射線AP,以點P為圓心,PA長為半徑畫弧,交AP的
延長線于點B;
②以點B為圓心,BA長為半徑畫弧,交l于點C(不與點A重合),連接BC;
③以點B為圓心,BP長為半徑畫孤,交BC于點Q;
④作直線PQ.
所以直線PQ就是所求作的直線.
根據小東設計的尺規作圖過程,
(1)使用直尺和圓規,補全圖形;(保留作圖痕跡)
(2)完成下面的證明
證明:∵PB=PA,BC= ,BQ=PB,
∴PB=PA=BQ= .
∴PQ∥l( )(填推理的依據).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com