【題目】如圖所示，在平面直角坐標系中，半徑均為1個單位長度的半圓O1、O2、O3，…組成一條平滑的曲線，點P從原點O出發，沿這條曲線向右運動，速度為每秒
個單位長度，則第2015秒時，點P的坐標是（ ）
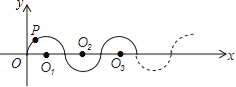
A. （2014，0） B. （2015，﹣1） C. （2015，1） D. （2016，0）
【答案】B
【解析】試題解析：半徑為1個單位長度的半圓的周長為： 
，
∵點P從原點O出發，沿這條曲線向右運動，速度為每秒
個單位長度，
∴點P1秒走
個半圓，
當點P從原點O出發，沿這條曲線向右運動，運動時間為1秒時，點P的坐標為（1，1），
當點P從原點O出發，沿這條曲線向右運動，運動時間為2秒時，點P的坐標為（2，0），
當點P從原點O出發，沿這條曲線向右運動，運動時間為3秒時，點P的坐標為（3，﹣1），
當點P從原點O出發，沿這條曲線向右運動，運動時間為4秒時，點P的坐標為（4，0），
當點P從原點O出發，沿這條曲線向右運動，運動時間為5秒時，點P的坐標為（5，1），
當點P從原點O出發，沿這條曲線向右運動，運動時間為6秒時，點P的坐標為（6，0），
…，
∵2015÷4=503…3
∴A2015的坐標是（2015，﹣1），
故選B．
應用題天天練四川大學出版社系列答案科目：初中數學 來源： 題型：
【題目】閱讀下面材料：
對于平面圖形A，如果存在一個圓，使圖形A上的任意一點到圓心的距離都不大于這個圓的半徑，則稱圖形A被這個圓所覆蓋.
對于平面圖形A，如果存在兩個或兩個以上的圓，使圖形A上的任意一點到其中某個圓的圓心的距離都不大于這個圓的半徑，則稱圖形A被這些圓所覆蓋.
例如：圖1中①的三角形被一個圓覆蓋，②中的四邊形被兩個圓所覆蓋.
回答下列問題：
(1)邊長為1 cm的正方形被一個半徑為r的圓所覆蓋，r的最小值是______ cm;
(2)邊長為1 cm的等邊三角形被一個半徑為r的圓所覆蓋，r的最小值是_____ cm;
(3)長為2 cm，寬為1 cm的矩形被兩個半徑均為r的圓所覆蓋，r的最小值是_____ cm.這兩個圓的圓心距是_____ cm.。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明和同桌小聰在課后復習時，對下面的一道思考題進行了認真的探索．
【思考題】如圖，一架2.5米長的梯子AB斜靠在豎直的墻AC上，這時點B到墻AC的距離為0.7米，如果梯子的頂端沿墻下滑0.4米，那么點B將向外移動________米．
解完【思考題】后，小聰提出了如下兩個問題：
(1)在【思考題】中，將“下滑0.4米”改為“下滑0.9米”，那么該題的答案會是0.9米嗎？為什么？
(2)在【思考題】中，梯子的頂端從A處沿墻AC下滑的距離與點B向外移動的距離，有可能相等嗎？為什么？
請你解答小聰提出的這兩個問題．
查看答案和解析>>
科目：初中數學 來源： 題型：
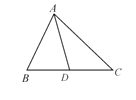
【題目】如圖所示，AD是△ABC的邊BC的中線.
(1)畫出以點D為對稱中心，與△ABD成中心對稱的三角形；
(2)若AB=10，AC=12，求AD長的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料：
解答“已知
，且
，
，確定
的取值范圍”有如下解，
解：∵，
∴
．
又∵，
∴
．
∴
．
又∵，
∴
，
①
同理得：
．②
由①
②得
．
∴的取值范圍是
．
請按照上述方法，完成下列問題：
（
）已知
，且
，
，求的取值范圍．
（
）已知
，
，若
，且
，求得取值范圍（結果用含
的式子表示）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，下列條件能保證△ABC≌△ADC的是：①AB=AD，BC=DC；②∠1=∠3，∠4=∠2；③∠1=∠2，∠4=∠3；④∠1=∠2，AB=AD；⑤∠1=∠2，BC=DC．（ ）
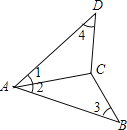
A. ①②③④⑤ B. ①②③④ C. ①③④ D. ①③④⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
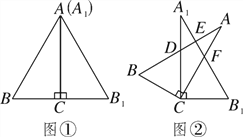
【題目】將兩塊相同的含30°角的直角三角板按圖①的方式放置，已知∠BAC＝∠B1A1C＝30°，AB＝2BC.固定三角板A1B1C，然后將三角板ABC繞點C順時針方向旋轉至圖②的位置，AB與A1C、A1B1分別交于點D、E，AC與A1B1交于點F.
(1)當旋轉角等于20°時，∠BCB1＝________度；
(2)當旋轉角等于多少度時，AB與A1B1垂直？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】
問題發現：如圖
，直線
是AB與AD之間的一點，連接
，可以發現
．
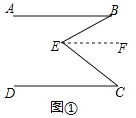
請把下面的證明過程補充完整：
證明：過點E作
，
已知
輔助線的作法
．
_____
______
同理
．
_____
等量代換
即
．
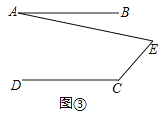
拓展探究：如果點E運動到圖
所示的位置，其他條件不變，進一步探究發現： 
，請說明理由．
解決問題：如圖
，請直接寫出
的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在對第一章“豐富的圖形世界”復習前，老師讓學生整理正方體截面的形狀并探究多面體（由若干個多邊形所圍成的幾何體）的棱數、面數、頂點數之間的數量關系，如圖是小穎用平面截正方體后剩余的多面體，請解答下列問題：
（1）根據上圖完成下表：
多面體 | V（頂點數） | F（面數） | E（棱數） |
（1） |
| 7 | 15 |
（3） | 6 |
| 9 |
（5） | 8 | 6 |
|
（2）猜想：一個多面體的V（頂點數），F（面數），E（棱數）之間的數量關系是 ；
（3）計算：已知一個多面體有20個面、30條棱，那么這個多面體有 個頂點．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com