
【題目】如圖(1),一平面直角坐標第xOy中,直線![]() 與y軸相交于點A,與反比例函數
與y軸相交于點A,與反比例函數![]() (x>0)的圖像相交于點B(m,2)
(x>0)的圖像相交于點B(m,2)
(1)求反比例函數的表達式;
(2)若將直線![]() 向上平移4個單位長度后與y軸交于點C,求ΔABC的面積;
向上平移4個單位長度后與y軸交于點C,求ΔABC的面積;
(3)如圖(2)將直線![]() 向上平移,與反比例函數的圖像交于點D,連接DA,DB.若
向上平移,與反比例函數的圖像交于點D,連接DA,DB.若
ΔABC的面積為3,求平移后直線的表達式。


圖(1) 圖(2)
【答案】(1)反比例函數的關系式是![]() ;(2)ΔABC的面積等于3;(3)平移后直線的表達式為
;(2)ΔABC的面積等于3;(3)平移后直線的表達式為![]()
【解析】試題分析:(1)先根據直線y=2x-1經過點B(m,2),求得B(1.5,2),再根據反比例函數y=![]() (x>0)的圖象經過點B,即可得到k的值;
(x>0)的圖象經過點B,即可得到k的值;
(2)過B作BH⊥y軸于H,根據AC=4,BH=1.5,即可得到△ABC的面積;
(3)設直線y=2x-1向上平移后與y軸交于點E,連接BE,過B作BM⊥y軸于M,則BM=1.5,根據DE∥AB,可得S△ABE=S△ABD=3,進而得到AE=4,再根據OA=1,可得OE=3,即可得出平移后直線的表達式為y=2x+3.
試題解析:
(1)∵直線![]() 經過點B(m,2)
經過點B(m,2)
∴![]() ,解得
,解得![]() ,∴點B的坐標是(
,∴點B的坐標是(![]() )
)
∵反比例函數![]() 的圖象經過點B(
的圖象經過點B(![]() ),∴
),∴![]()
∴反比例函數的關系式是![]()
(2)過點B作BH⊥y軸于點H
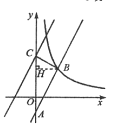
根據題意,得AC=4
由(1),得點B的坐標為(![]() )
)
∴![]() ,
,
∴![]()
∴ΔABC的面積等于3
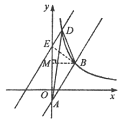
(3)設直線![]() 向上平移后與y軸交于點E,連接BE,過點B作
向上平移后與y軸交于點E,連接BE,過點B作
BM⊥y軸于點M,則![]() 。
。
∵DE∥AB,ΔABD的面積為3.
∴![]()
∴![]() ,即
,即![]() ,
,
∴AE=4。
∵OA=1,
∴OE=3
∴平移后直線的表達式為![]()


科目:初中數學 來源: 題型:
【題目】已知:四邊形ABCD,E,F,G,H是各邊的中點.
(1)求證:四邊形EFGH是平行四邊形;
(2)假如四邊形ABCD是一個矩形,猜想四邊形EFGH是什么圖形?并證明你的猜想.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電業局要對某市區的電線路進行巡檢,某檢修小組從A地出發,在東西向的馬路上檢修線路,如果規定向東行駛為正,向西行駛為負,檢修車一天中八次行駛記錄如下:(單位:km)-4,+7,-9,+8,+6,-5,-2,-4
(1)求收工時檢修小組在A地的什么方向?距A地多遠?
(2)若每千米耗油0.5升,當維修小組返回到A地時,問共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在RtΔABC中,AB=AC=4,∠BAC=900.點E為AB的中點,以AE為對角線作正方形ADEF,連接CF并延長交BD于點G,則線段CG的長等于________________.
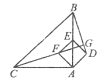
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點A,B在數軸上分別表示有理數a,b.A,B兩點之間的距離表示為AB,在數軸上A,B兩點之間的距離AB=|a﹣b|.利用數形結合思想回答下列問題:
(1)數軸上表示﹣2和8兩點之間的距離是________.
(2)數軸上表示x和﹣4兩點A和B之間的距離表示為__________;如果AB=2,那么x=___________.
(3)若點C表示的數為x,當點C在什么位置時,|![]() x+1|+|
x+1|+|![]() x1|取得的值最小,并直接寫出最小值。
x1|取得的值最小,并直接寫出最小值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐
問題情境
如圖,同學們用矩形紙片ABCD開展數學探究活動,其中AD=8,CD=6。
操作計算
(1)如圖(1),分別沿BE,DF剪去RtΔABE和RtΔCDF兩張紙片,如果剩余的紙片BEDF菱形,求AE的長;

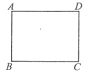
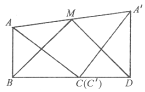
圖(1) 圖(2) 圖(3)
操作探究
把矩形紙片ABCD沿對角線AC剪開,得到ΔABC和![]() 兩張紙片
兩張紙片
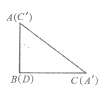
(2)將兩張紙片如圖(2)擺放,點C和![]() 重合,點B,C,D在同一條直線上,連接
重合,點B,C,D在同一條直線上,連接![]() ,記
,記![]() 的中點為M,連接BM,MD,發現ΔBMD是等腰三角形,請證明:
的中點為M,連接BM,MD,發現ΔBMD是等腰三角形,請證明:
(3)如圖(3),將兩張紙片疊合在一起,然后將![]() 紙片繞點B順時針旋轉a(00<a<900),連接
紙片繞點B順時針旋轉a(00<a<900),連接![]() 和
和![]() ,探究并直接寫出線段
,探究并直接寫出線段![]() 與
與![]() 的關系。
的關系。
查看答案和解析>>
科目:初中數學 來源: 題型:
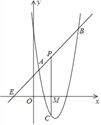
【題目】如圖,直線y=x+2與拋物線y=ax2+bx+6相交于A(![]() ,
,![]() )和B(4,m),點P是AB上的動點,設點P的橫坐標為n,過點P作PC⊥x軸,交拋物線于點C,與x軸交于M點.
)和B(4,m),點P是AB上的動點,設點P的橫坐標為n,過點P作PC⊥x軸,交拋物線于點C,與x軸交于M點.
(1)求拋物線的表達式;
(2)點P是線段AB上異于A,B的動點,是否存在這樣的點P,使線段PC的長有最大值?若存在,求出這最大值,若不存在,請說明理由;
(3)點P在直線AB上自由移動,當三個點C,P,M中恰有一點是其它兩點所連線段的中點時,請直接寫出m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
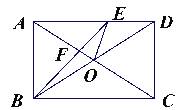
【題目】如圖,在矩形ABCD中,對角線AC、BD交于點O,BE平分∠ABC交AC于點F,交AD于點E,且∠DBF=15°,求證:(1)AO=AE; (2)∠FEO的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖△ABC中,點D是邊AB的中點,CE∥AB,且AB=2CE,連結BE、CD。

(1)求證:四邊形BECD是平行四邊形;
(2)用無刻度的直尺畫出△ABC邊BC上的中線AG(保留畫圖痕跡)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com