
【題目】如圖1,正方形ABCD中,AB=4cm,點P從點D出發沿DA向點A勻速運動,速度是1cm/s,同時,點Q從點A出發沿AB方向,向點B勻速運動,速度是2cm/s,連接PQ、CP、CQ,設運動時間為t(s)(0<t<2)
(1)是否存在某一時刻t,使得PQ∥BD?若存在,求出t值;若不存在,說明理由
(2)設△PQC的面積為s(cm2),求s與t之間的函數關系式;
(3)如圖2,連接AC,與線段PQ相交于點M,是否存在某一時刻t,使S△QCM:S△PCM=3:5?若存在,求出t值;若不存在,說明理由.

【答案】(1)![]() ;(2)S=t2﹣2t+8(0<t<2);(3)
;(2)S=t2﹣2t+8(0<t<2);(3)![]() .
.
【解析】
由題意可得:由運動知,DP=t,AQ=2t,得出AP=4-t,BQ=4-2t,
(1)判斷出AQ=AP,得出2t=4-t,即可;
(2)直接利用面積的和差即可得出結論;
(3)先判斷![]() =
=![]() ,再得到
,再得到![]() ,從而得出
,從而得出![]() 解方程即可得出結論.
解方程即可得出結論.
解:∵四邊形ABCD是正方形,
∴AB=BC=CD=AD=4,
由運動知,DP=t,AQ=2t,
∴AP=4﹣t,BQ=4﹣2t,
(1)連接BD,如圖1,
∵AB=AD,
∴∠ABD=∠ADB,
∵PQ∥BD,
∴∠ABD=∠AQP,∠APQ=∠ADB,
∴∠APQ=∠AQP,
∴AQ=AP,
∴2t=4﹣t,
∴t=![]() ;
;
(2)S=S正方形ABCD﹣S△APQ﹣S△BCQ﹣S△CDP
=AB2﹣![]() AQ×AP﹣
AQ×AP﹣![]() BQ×BC﹣
BQ×BC﹣![]() DP×CD
DP×CD
=16﹣![]() ×2t×(4﹣t)﹣
×2t×(4﹣t)﹣![]() ×(4﹣2t)×4﹣
×(4﹣2t)×4﹣![]() t×4
t×4
=16+t2﹣4t﹣8+4t﹣2t
=t2﹣2t+8(0<t<2);
(3)如圖2,
過點C作CN⊥PQ于N,
∴S△MCQ=![]() MQ×CN,S△MCP=
MQ×CN,S△MCP=![]() MP×CN,
MP×CN,
∵S△QCM:S△PCM=3:5,
∴![]() =
=![]() ,
,
∴![]() ,
,
過點M作MG⊥AB于G,MH⊥AD于H,
∵點M是正方形ABCD的對角線AC上的一點,
∴MG=MH,
∴S△AMQ=![]() AQ×MG,S△APM=
AQ×MG,S△APM=![]() AP×MH,
AP×MH,
∴![]()
∴![]()
∴t=![]() .
.


科目:初中數學 來源: 題型:
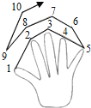
【題目】 從大拇指開始,按照大拇指→食指→中指→無名指→小指→無名指→中指→食指→大拇指→食指……的順序,依次數整數1、2、3、4、5,6、7、…,當數到4019時對應的手指為_____;當第n次數到無名指時,數到的數是_____(用含n的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“十·一”黃金周期間,武漢動物園在7天假期中每天旅游的人數變化如下表(正數表示比前一天多的人數,負數表示比前一天少的人數)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人數變化單位:萬人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若9月30日的游客人數記為![]() ,請用
,請用![]() 的代數式表示10月2日的游客人數?
的代數式表示10月2日的游客人數?
(2)請判斷七天內游客人數最多的是哪天?請說明理由。
(3)若9月30日的游客人數為2萬人,門票每人10元。問黃金周期間武漢動物園門票收入是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的個數是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的個數是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如下數表是由1開始的連續自然數組成的,觀察規律并完成各題的解答.

(1)表示第9行的最后一個數是 .
(2)用含n的代數式表示:第n行的第一個數是 ,第n行共有 個數;第n行各數之和是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解學校開展“孝敬父母,從家務勞動做起”活動的實施情況,該校抽取八年級50名學生,調查他們一周(按七天計算)做家務所用時間(單位:小時)得到一組數據,繪制成下表:
時間x(小時) | 劃記 | 人數 | 所占百分比 |
0.5x≤x≤1.0 | 正正 | 14 | 28% |
1.0≤x<1.5 | 正正正 | 15 | 30% |
1.5≤x<2 |
| 7 |
|
2≤x<2.5 |
| 4 | 8% |
2.5≤x<3 | 正 | 5 | 10% |
3≤x<3.5 |
| 3 |
|
3.5≤x<4 |
|
| 4% |
合計 | 50 | 100% |
(1)請填表中未完成的部分;
(2)根據以上信息判斷,每周做家務的時間不超過1.5小時的學生所占的百分比是多少?
(3)針對以上情況,寫出一個20字以內的倡導“孝敬父母,熱愛勞動”的句子.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在研究位似問題時,甲、乙同學的說法如下:
甲:如圖①,已知矩形ABCD和矩形EFGO在平面直角坐標系中,點B,F的坐標分別為(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似圖形,點P(點P在GC上)是位似中心,則點P的坐標為(0,2).
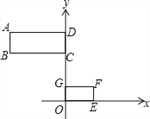
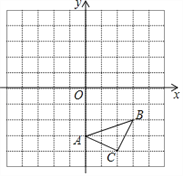
圖① 圖②
乙:如圖②,正方形網格中,每個小正方形的邊長是1個單位長度,以點C為位似中心,在網格中畫△A1B1C1,使△A1B1C1與△ABC位似,且△A1B1C1與△ABC的位似比為2:1,則點B1的坐標為(4,0).
對于兩人的觀點,下列說法正確的是( )
A. 兩人都對 B. 兩人都不對 C. 甲對乙不對 D. 甲不對乙對
查看答案和解析>>
科目:初中數學 來源: 題型:
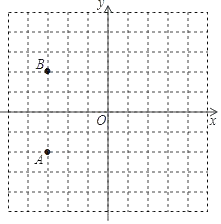
【題目】如圖,在直角坐標系中,已知點O,A的坐標分別為(0,0),(﹣3,﹣2).
(1)點B的坐標是 ,點B與點A的位置關系是 .現將點B,點A都向右平移5個單位長度分別得到對應點C和D,順次連接點A,B,C,D,畫出四邊形ABCD;
(2)橫、縱坐標都是整數的點成為整數點,在四邊形ABCD內部(不包括邊界)的整數點M使S△ABM=8,請直接寫出所有點M的可能坐標;
(3)若一條經過點(0,﹣4)的直線把四邊形ABCD的面積等分,則這條直線的表達式是 ,并在圖中畫出這條直線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一條筆直的公路依次經過A,B,C三地,且A,B兩地相距1000m,B,C兩地相距2000m.甲、乙兩人騎車分別從A,B兩地同時出發前往C地.
(1)若甲每分鐘比乙多騎100m,且甲、乙同時到達C地 ,求甲的速度;
(2)若出發5 min,甲還未騎到B地,且此時甲、乙兩人相距不到650m,請判斷誰先到達C地,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com