
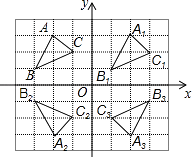
【題目】如圖,△ABC中,A(﹣2,3),B(﹣3,1),C(﹣1,2). 
(1)①將△ABC向右平移4個單位長度,畫出平移后的△A1B1C1;
②畫出△ABC關于x軸對稱的△A2B2C2;
③將△ABC繞原點O旋轉180°,畫出旋轉后的△A3B3C3;
(2)在△A1B1C1 , △A2B2C2 , △A3B3C3中,△與△成軸對稱,對稱軸是;△與△成中心對稱,對稱中心的坐標是 .
【答案】
(1)解:①△A1B1C1如圖所示
②△A2B2C2如圖所示
③△A3B3C3如圖所示
(2)A2B2C2 ;A3B3C3 ;y軸;A1B1C1 ;A3B3C3 ;(2,0)
【解析】解:(1)如圖所示;(2)由圖可知:△A2B2C2與△A3B3C3呈軸對稱,且對稱軸為y軸;
△A1B1C1與△A3B3C3呈中心對稱,且對稱中心為(2,0).
所以答案是:A2B2C2 , A3B3C3 , y軸;A1B1C1 , A3B3C3 , (2,0).
【考點精析】根據題目的已知條件,利用作軸對稱圖形的相關知識可以得到問題的答案,需要掌握畫對稱軸圖形的方法:①標出關鍵點②數方格,標出對稱點③依次連線.


科目:初中數學 來源: 題型:
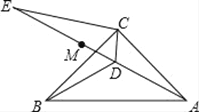
【題目】如圖,在△ABC中,AC=BC,∠ACB=90°,點D為△ABC內一點,且BD=AD.
(1)求證:CD⊥AB;
(2)∠CAD=15°,E為AD延長線上的一點,且CE=CA.
①求證:DE平分∠BDC;
②若點M在DE上,且DC=DM,請判斷ME、BD的數量關系,并給出證明;
③若N為直線AE上一點,且△CEN為等腰三角形,直接寫出∠CNE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 從
從![]() 出發以每秒
出發以每秒![]() 個單位的速度在線段
個單位的速度在線段![]() 上從點
上從點![]() 向點
向點![]() 運動,點
運動,點![]() 同時從
同時從![]() 出發以每秒
出發以每秒![]() 個單位的速度在線段
個單位的速度在線段![]() 上向點
上向點![]() 運動,連接
運動,連接![]() 、
、![]() ,設
,設![]() 、
、![]() 兩點運動時間為
兩點運動時間為![]() 秒
秒![]() .
.
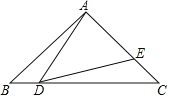
(1)運動 秒時,![]() ;
;
(2)運動多少秒時,![]() ≌
≌![]() 能成立;
能成立;
(3)若![]() ≌
≌![]() ,
,![]() ,求
,求![]() 的大小.(用含
的大小.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(9分)如圖,在平面直角坐標系中,Rt△ABC的三個頂點分別是A(-3,2),B(0,4),C(0,2).
(1)將△ABC以點C為旋轉中心旋轉180°,畫出旋轉后對應的△A1B1C;平移△ABC,若A的對應點A2的坐標為(0,4),畫出平移后對應的△A2B2C2;
(2)若將△A1B1C繞某一點旋轉可以得到△A2B2C2,請直接寫出旋轉中心的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
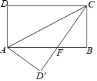
【題目】如圖,長方形ABCD中,AB=8,BC=4,將長方形沿AC折疊,點D落在D′處.
(1)求證:△AFD′≌△CFB;
(2)求線段BF的長度;
(3)試求出重疊部分△AFC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c的圖象的一部分,對稱軸是直線x=1.
①b2>4ac;
②4a+2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是拋物線上的兩點,則y1<y2 .
上述4個判斷中,正確的是( )
A.①②
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的一元函數y=﹣2x+m和反比例函數y= ![]() 的圖象都經過點A(﹣2,1).
的圖象都經過點A(﹣2,1).
(1)求一次函數和反比例函數的解析式;
(2)求一次函數與反比例函數的另一個交點B的坐標;
(3)求△AOB的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com