
【題目】如圖,點A,D是函數y= ![]() (k>0,x>0)圖象上兩點(點A在點D的左側),直線AD分別交x,y軸于點E,F.AB⊥x軸于點B,CD⊥x軸于點C,連結AO,BD.若BC=OB+CE,S△AOF+S△CDE=1,則S△ABD= .
(k>0,x>0)圖象上兩點(點A在點D的左側),直線AD分別交x,y軸于點E,F.AB⊥x軸于點B,CD⊥x軸于點C,連結AO,BD.若BC=OB+CE,S△AOF+S△CDE=1,則S△ABD= . 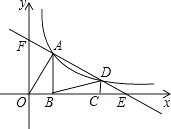
【答案】![]()
【解析】解:設A(a, ![]() ),D(d,
),D(d, ![]() ),則d>a,B(a,0),C(d,0), ∵BC=d﹣a,BC=OB+CE,
),則d>a,B(a,0),C(d,0), ∵BC=d﹣a,BC=OB+CE,
∴OE=2BC=2d﹣2a,
∴E(2d﹣2a,0).
∵tan∠AEB= ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
整理得3a2﹣4ad+d2=0,
(a﹣d)(3a﹣d)=0,
∵a﹣d≠0,
∴3a﹣d=0,
∴d=3a.
∵ ![]() =
= ![]() ,
,
∴OF= ![]() .
.
∵S△AOF+S△CDE=1,
∴ ![]() ×
× ![]() ×a+
×a+ ![]() ×(2d﹣2a﹣d)×
×(2d﹣2a﹣d)× ![]() =1,
=1,
∴k= ![]() ,
,
∴S△ABD=S梯形ABCD﹣S△BCD
= ![]() (
( ![]() +
+ ![]() )(d﹣a)﹣
)(d﹣a)﹣ ![]() ×
× ![]() ×(d﹣a)
×(d﹣a)
= ![]() ×
× ![]() ×(d﹣a)
×(d﹣a)
= ![]() ×
× ![]() ×(3a﹣a)
×(3a﹣a)
= ![]() .
.
所以答案是 ![]() .
.
【考點精析】認真審題,首先需要了解比例系數k的幾何意義(幾何意義:表示反比例函數圖像上的點向兩坐標軸所作的垂線段與兩坐標軸圍成的矩形的面積).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
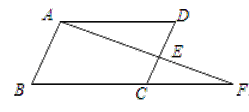
【題目】如圖,根據圖形填空:
已知:∠DAF=∠F,∠B=∠D,AB與DC平行嗎?
解:∠DAF=∠F ( )
∴AD∥BF( ),
∴∠D=∠DCF( )
∵∠B=∠D ( )
∴∠B=∠DCF ( )
∴AB∥DC( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,四邊形ABCD中,對角線AC,BD相交于點O,AB=AC=AD,∠DAC=∠ABC. 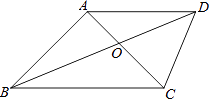
(1)求證:BD平分∠ABC;
(2)若∠DAC=45°,OA=1,求OC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
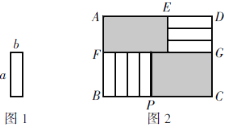
【題目】將7張如圖1所示的長為a,寬為b(a>b)的小長方形紙片按圖2所示的方式不重疊地放在長方形ABCD內,未被覆蓋的部分(兩個長方形)用陰影表示.設左上角與右下角的陰影部分的面積的差為S,當BC的長度變化時,按照同樣的放置方式,S始終保持不變,求a,b滿足的條件.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學九(1)班為了了解全班學生喜歡球類活動的情況,采取全面調查的方法,從足球、乒乓球、籃球、排球等四個方面調查了全班學生的興趣愛好,根據調查的結果組建了4個興趣小組,并繪制成如圖所示的兩幅不完整的統計圖(如圖①,②,要求每位學生只能選擇一種自己喜歡的球類),請你根據圖中提供的信息解答下列問題: 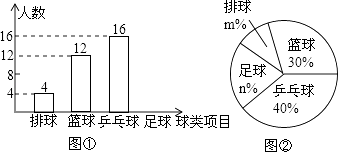
(1)九(1)班的學生人數為 , 并把條形統計圖補充完整;
(2)扇形統計圖中m= , n= , 表示“足球”的扇形的圓心角是度;
(3)排球興趣小組4名學生中有3男1女,現在打算從中隨機選出2名學生參加學校的排球隊,請用列表或畫樹狀圖的方法求選出的2名學生恰好是1男1女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司有![]() 、
、![]() 兩種型號的客車共20輛,它們的載客量、每天的租金如下表所示.已知在20輛客車都坐滿的情況下,共載客720人.
兩種型號的客車共20輛,它們的載客量、每天的租金如下表所示.已知在20輛客車都坐滿的情況下,共載客720人.
A型號客車 | B型號客車 | |
載客量(人/輛) | 45 | 30 |
租金(元/輛) | 600 | 450 |
(1)求![]() 、
、![]() 兩種型號的客車各有多少輛?
兩種型號的客車各有多少輛?
(2)某中學計劃租用![]() 、
、![]() 兩種型號的客車共8輛,同時送七年級師生到沙家浜參加社會實踐活動,已知該中學租車的總費用不超過4600元. 求最多能租用多少輛A型號客車?
兩種型號的客車共8輛,同時送七年級師生到沙家浜參加社會實踐活動,已知該中學租車的總費用不超過4600元. 求最多能租用多少輛A型號客車?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AC=6,BC=8,點D、M分別在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜邊都在AB上,則五個小直角三角形的周長和為 . 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com