
【題目】如圖,矩形ABCD的對角線AC,BD相交于點O,點E,F,M,N分別為OA,OB,OC,OD的中點,連接EF,FM,MN,NE. 
(1)依題意,補全圖形;
(2)求證:四邊形EFMN是矩形;
(3)連接DM,若DM⊥AC于點M,ON=3,求矩形ABCD的面積.
【答案】
(1)解:如圖所示:
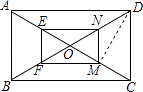
(2)證明:∵點E,F分別為OA,OB的中點,
∴EF∥AB,EF= ![]() AB,
AB,
同理:NM∥CD,MN= ![]() DC,
DC,
∵四邊形ABCD是矩形,
∴AB∥DC,AB=DC,AC=BD,
∴EF∥NM,EF=MN,
∴四邊形EFMN是平行四邊形,
∵點E,F,M,N分別為OA,OB,OC,OD的中點,
∴EO= ![]() AO,MO=
AO,MO= ![]() CO,
CO,
在矩形ABCD中,AO=CO= ![]() AC,BO=DO=
AC,BO=DO= ![]() BD,
BD,
∴EM=EO+MO= ![]() AC,
AC,
同理可證FN= ![]() BD,
BD,
∴EM=FN,
∴四邊形EFMN是矩形
(3)解:∵DM⊥AC于點M,
由(2)MO= ![]() CO,
CO,
∴DO=CD,
在矩形ABCD中,
AO=CO= ![]() AC,BO=DO=
AC,BO=DO= ![]() BD,AC=BD,
BD,AC=BD,
∴AO=BO=CO=DO,
∴△COD是等邊三角形,
∴∠ODC=60°,
∵MN∥DC,
∴∠FNM=∠ODC=60°,
在矩形EFMN中,∠FMN=90°.
∴∠NFM=90°﹣∠FNM=30°,
∵NO=3,
∴FN=2NO=6,FM=3 ![]() ,MN=3,
,MN=3,
∵點F,M分別為OB,OC的中點,
∴BC=2FM=6 ![]() ,
,
∴矩形的面積為BCCD=36 ![]()
【解析】(1)根據題目要求畫出圖形即可;(2)根據三角形中位線定理可得EF∥AB,EF= ![]() AB,NM∥CD,MN=
AB,NM∥CD,MN= ![]() DC,再由矩形的性質可得AB∥DC,AB=DC,AC=BD,進而可得四邊形EFMN是矩形;(3)根據條件可得DM垂直平分OC,進而可得DO=CO,然后證明△COD是等邊三角形,進而得出BC,CD的長,進而得出答案.
DC,再由矩形的性質可得AB∥DC,AB=DC,AC=BD,進而可得四邊形EFMN是矩形;(3)根據條件可得DM垂直平分OC,進而可得DO=CO,然后證明△COD是等邊三角形,進而得出BC,CD的長,進而得出答案.


科目:初中數學 來源: 題型:
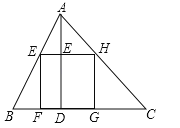
【題目】若正方形有兩個相鄰頂點在三角形的同一條邊上,其余兩個頂點分別在三角形的另兩條邊上,則正方形稱為三角形該邊上的內接正方形,△ABC中,設BC=a,AC=b,AB=c,各邊上的高分別記為![]() ,
,![]() ,
,![]() ,各邊上的內接正方形的邊長分別記為
,各邊上的內接正方形的邊長分別記為![]() ,
,![]() ,
,![]() .
.
(1)模擬探究:如圖,正方形EFGH為△ABC的BC邊上的內接正方形,求證:![]() ;
;
(2)特殊應用:若∠BAC=90°,![]() =
=![]() =2,求
=2,求![]() 的值;
的值;
(3)拓展延伸:若△ABC為銳角三角形,b<c,請判斷![]() 與
與![]() 的大小,并說明理由.
的大小,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】去年,中央財政安排資金 8 200 000 000 元,免除城市義務教育學生學雜費,支持進城務工人員隨遷子女公平接受義務教育,這個數據用科學記數法可表示為元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】具備下列條件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A= ![]() ∠B=
∠B= ![]() ∠C
∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=2∠B=3∠C
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com