Question

【題目】如圖1，已知，分別為兩坐標軸上的點，且，滿足，且.

（1）求、、三點的坐標；

（2）若，過點的直線分別交、于、兩點，且，設、兩點的橫坐標分別為、，求的值；

（3）如圖2，若，點是軸上點右側一動點，于點，在上取點，使，連接，當點在點右側運動時，的度數是否改變?若不變，請求其值；若改變，請說明理由.

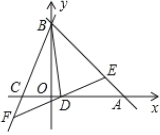
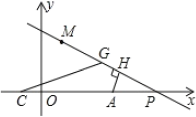
圖1 圖2

Answer 1

【答案】(1) A(12,0),B(0,12)，C(4,0)；

(2)

(3) 不改變，

【解析】

（1）由偶次方和絕對值的非負性質求出a和b的值，得出點A、B的坐標，再求出OC，即可得出點C的坐標；
（2）作EG⊥x軸于G，FH⊥x軸于H，DF=DE，由AAS證明△FDH≌△EDG，得出DH=DG，即可得出結果；
（3）連接MA、MC，過C作CT⊥PM于T，證明△CMT≌△MAH，可證明△CGT是等腰直角三角形，可求得∠CGM=45°．

(1)∵，

∴a12=0，b12=0，

∴a=b=12，

∴A(12,0),B(0,12)，

∴OA=OB=12，

∵.

∴OC=4，

∴C(4,0)；

(2)作EG⊥x軸于G，FH⊥x軸于H，如圖1所示：

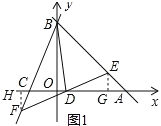
則

在△FDH和△EDG中,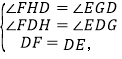

∴△FDH≌△EDG(AAS)，

∴DH=DG,即

∴

(3)∠CGM的度數不改變,

如圖3，連接MA、MC，過C作CT⊥PM于T，過M作MS⊥x軸于點S，

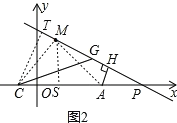
∵M(4,8),C(4,0),A(12,0)，

∴S(4,0)，

∴MS垂直平分AC，

∴MC=MA，且MS=SC，

∴

∴

∴∠TCM=∠AMH，

在△CMT和△MAH中

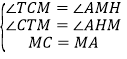
∴△CMT≌△MAH(AAS)，

∴TM=AH，CT=MH，

又AH=HG，

∴MT=GH，

∴GT=GM+MT=MG+GH=MH=CT，

∴△CGT是等腰直角三角形，

∴

即當點P在點A右側運動時，∠CGM的度數不改變.