【題目】二次函數y=ax2+bx+c（a≠0）的圖象如圖．對稱軸x=﹣1．下列結論：
①4ac﹣b2＜0；②4a+c＜2b；③3b+2c＜0．
其中正確結論的個數是（ ）
A. 3個 B. 2個 C. 1個 D. 0個
科目：初中數學 來源： 題型：
【題目】如圖，已知：關于x的二次函數
的圖象與x軸交于點A(1，0)和點B，與y軸交于點C(0，3)，拋物線的對稱軸與x軸交于點D.
(1)求二次函數的表達式；
(2)在y軸上是否存在一點P，使△PBC為等腰三角形.若存在，請求出點P的坐標；
(3)有一個點M從點A出發，以每秒1個單位的速度在AB上向點B運動，另一個點N從點D與點M同時出發，以每秒2個單位的速度在拋物線的對稱軸上運動，當點M到 達點B時，點M、N同時停止運動，問點M、N運動到何處時，△MNB面積最大，試求出最大面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
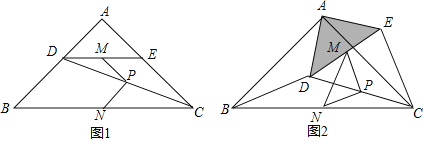
【題目】如圖1，在Rt△ABC中，∠A＝90°，AB＝AC，點D，E分別在邊AB，AC上，AD＝AE，連接DC，點M，P，N分別為DE，DC，BC的中點．
（1）觀察猜想
圖1中，線段PM與PN的數量關系是 ，位置關系是 ；
（2）探究證明
把△ADE繞點A逆時針方向旋轉到圖2的位置，連接MN，BD，CE，判斷△PMN的形狀，并說明理由；
（3）拓展延伸
把△ADE繞點A在平面內自由旋轉，若AD＝4，AB＝10，請直接寫出△PMN面積的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】通過小學的學習我們知道，分數可分為“真分數”和“假分數”，并且假分數都可化為帶分數．類比分數，對于分式也可以定義：對于只含有一個字母的分式，當分子的次數大于或等于分母的次數時，我們稱之為“假分式”；當分子的次數小于分母的次數時，我們稱之為“真分式”．類似的，假分式也可以化為帶分式（即：整式與真分式的和的形式）．
如：
解決下列問題：
（1）分式
是________分式（填“真”或“假”）；
（2）假分式
可化為帶分式_________的形式；請寫出你的推導過程；
（3）如果分式的值為整數，那么
的整數值為_________．
查看答案和解析>>
科目：初中數學 來源： 題型：
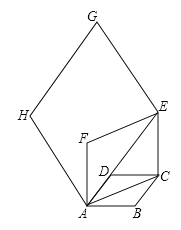
【題目】如圖，邊長為
的菱形
中，
．連結對角線
，以為邊作第二個菱形
，使
．連結
，再以為邊作第三個菱形
，使
，一按此規律所作的第
個菱形的邊長是__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，平行四邊形OABC的頂點A在x軸上，頂點B的坐標為（4，6），直線y=kx+3k將平行四邊形OABC分割成面積相等的兩部分，則k的值是（ ）.
A．
B．
C．-
D．﹣
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】鄂州市化工材料經銷公司購進一種化工原料若干千克，價格為每千 克30元．物價部門規定其銷售單價不高于每千克60元，不低于每千克30元．經市場調查發現：日銷售量y（千克）是銷售單價x（元）的一次函數，且當x=60時 ，y=80；x=50時，y=100．在銷售過程中，每天還要支付其他費用450元．
（1）（3分）求出y與x的函數關系式，并寫出自變量x的取值范圍．
（2）（3分）求該公司銷售該原料日獲利w（元）與銷售單價x（元）之間的函數關系式．
（3）（4分）當銷售單價為多少元時，該公司日獲利最大？最大獲利是多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“滴滴出行”改變了傳統打車方式，最大化節省了司機與乘客雙方的資源與時間．該打車方式的總費用由里程費和耗時費組成，其中里程費按
元
公里計算，耗時費按
元分鐘計算．甲、乙兩乘客用該打車方式出行，按上述計價規則，其打車總費用、行駛里程數與平均車速等信息如下表：
平均速度（公里/時） | 里程數（公里） | 車費（元） | |
甲乘客 |
|
|
|
乙乘客 |
|
|
|
（1）求，的值；
（2）如果你采用“滴滴出行”的打車方式，保持平均車速
公里時，行駛了
公里，那么你是否能夠計算出打車的總費用？如果能，總費用為多少元？如果不能，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
