
【題目】點![]() ,
,![]() 在數軸上分別表示有理數
在數軸上分別表示有理數![]() ,
,![]() ,
,![]() ,
,![]() 兩點之間的距離表示為
兩點之間的距離表示為![]() ,在數軸上
,在數軸上![]() ,
,![]() 兩點之間的距離
兩點之間的距離![]() .已知數軸上
.已知數軸上![]() ,
,![]() 兩點表示數
兩點表示數![]() ,
,![]() 滿足
滿足![]() ,點
,點![]() 為數軸上一動點,其對應的數為
為數軸上一動點,其對應的數為![]() .
.
![]()
(1)![]() ,
,![]() 兩點之間的距離是.
兩點之間的距離是.
(2)![]() 與
與![]() 之間的距離表示為.
之間的距離表示為.
(3)數軸上是否存在點![]() ,使點
,使點![]() 到點
到點![]() ,點
,點![]() 的距離之和為
的距離之和為![]() ?若存在,請求出
?若存在,請求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
(4)現在點![]() ,點
,點![]() 分別以
分別以![]() 單位/秒和
單位/秒和![]() 單位/秒的速度同時向右運動,當點
單位/秒的速度同時向右運動,當點![]() 與點
與點![]() 之間的距離為
之間的距離為![]() 個單位長度時,求點
個單位長度時,求點![]() 所對應的數是多少?
所對應的數是多少?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() ;(4)點A所對應的數是
;(4)點A所對應的數是![]() 或14.
或14.
【解析】
(1)根據絕對值的非負性求出a,b,即可得到A,B之間的距離;
(2)在數軸上A、B兩點之間的距離為AB=|a-b|,依此即可求解;
(3)分兩種情況:點P在點A的左邊,點P在點B的右邊,進行討論即可求解;
(4)分兩種情況:點A在點B的左邊,點A在點B的右邊,進行討論即可求解.
(1)∵![]()
∴a=-2,b=6,
∴A點表示的數為-2,B點表示的數為6,
A,B之間的距離為![]()
(2)x與4之間的距離表示為|x(4)|=|x+4|
(3)點P在點A的左邊時:16=-2-x+6-x,解得x=-6,
點P在點B的右邊時:16=x-(-2)+x-6,解得x=10,
∴x的值為![]() 或
或![]() ;
;
(4)當點A在點B的左邊,設運動時間為t,
(6+0.5t)-(-2+2t)=4,解得t=![]()
點A所對應的數是![]()
當點A在點B的右邊,設運動時間為t,
(-2+2t) - (6+0.5t)=4,解得t=8
點A所對應的數是14
故點A所對應的數是![]() 或14.
或14.


科目:初中數學 來源: 題型:
【題目】已知a是最大的負整數,b是-5的相反數,c=![]() ,且a、b、c分別是點A、B、C在數軸上對應的數.若動點P從點A出發沿數軸正方向運動,動點Q同時從點B出發也沿數軸正方向運動,點P的速度是每秒3個單位長度,點Q的速度是每秒1個單位長度.
,且a、b、c分別是點A、B、C在數軸上對應的數.若動點P從點A出發沿數軸正方向運動,動點Q同時從點B出發也沿數軸正方向運動,點P的速度是每秒3個單位長度,點Q的速度是每秒1個單位長度.
![]()
(1)求a、b、c的值;
(2)P、Q同時出發,求運動幾秒后,點P可以追上點Q?
(3)在(2)的條件下,P、Q出發的同時,動點M從點C出發沿數軸正方向運動,速度為每秒6個單位長度,點M追上點Q后立即返回沿數軸負方向運動,追上后點M再運動幾秒,M到Q的距離等于M到P距離的兩倍?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在平面直角坐標系中,拋物線![]() 與x軸相交于點A,B,與y軸相交于點C. 已知A,C兩點的坐標分別為A(-4,0), C(0,4).
與x軸相交于點A,B,與y軸相交于點C. 已知A,C兩點的坐標分別為A(-4,0), C(0,4).
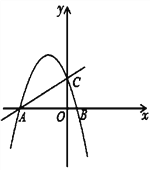
(1)求拋物線的表達式;
(2)如果點P,Q在拋物線上(P點在對稱軸左邊),且PQ∥AO,PQ=2AO,求P,Q的坐標;
(3)動點M在直線y=x+4上,且△ABC與△COM相似,求點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
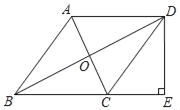
【題目】如圖,O為△ABC邊AC的中點,AD∥BC交BO的延長線于點D,連接DC,DB平分∠ADC,作DE⊥BC,垂足為E.
(1)求證:四邊形ABCD為菱形;
(2)若BD=8,AC=6,求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】勾股定理是幾何學中的明珠,充滿著魅力,千百年來,人們對它趨之若鶩,其中有著名的數學家,也有業余數學愛好者,向常春在1994年構造發現了一個新的證法:把兩個全等的直角三角形如圖1放置,其三邊長分別為a、b、c,顯然∠DAB=∠B=90°,AC⊥DE.
(1)請用a、b、c分別表示出梯形ABCD、四邊形AECD、△EBC的面積,再通過探究這三個圖形面積之間的關系,證明:勾股定理a2+b2=c2;
(2)如圖2,鐵路上A、B兩點(看作直線上的兩點)相距40千米,C、D為兩個村莊(看作兩個點),AD⊥AB,BC⊥AB,垂足分別為A、B,AD=24千米,BC=16千米,在AB上有一個供應站P,且PC=PD,求出AP的距離;
(3)借助(2)的思考過程與幾何模型,直接寫出代數式![]() 的最小值為 .
的最小值為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了調查市場上某品牌方便面的色素含量是否符合國家標準,工作人員在超市里隨機抽取了某品牌的方便面進行檢驗.圖1和圖2是根據調查結果繪制的兩幅不完整的統計圖,其中A、B、C、D分別代表色素含量為0.05%以下、0.05%~0.1%、0.1%~0.15%、0.15%以上,圖1的條形圖表示的是抽查的方便面中色素含量分布的袋數,圖2的扇形圖表示的是抽查的方便面中色素的各種含量占抽查總數的百分比.請解答以下問題:
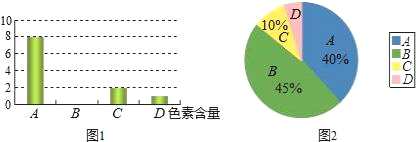
(1)本次調查一共抽查了多少袋方便面?
(2)將圖1中色素含量為B的部分補充完整;
(3)圖2中的色素含量為D的方便面所占的百分比是多少?
(4)若色素含量超過0.15%即為不合格產品,某超市這種品牌的方便面共有10000袋,那么其中不合格的產品有多少袋?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O、H分別為邊AB、AC的中點,將△ABC繞點B順時針旋轉120°到△A1BC1的位置,則整個旋轉過程中線段OH所掃過部分的面積(即陰影部分面積)為_____.
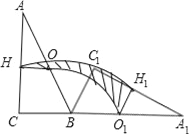
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某景區一電瓶小客車接到任務從景區大門出發,向東走2千米到達A景區,繼續向東走2.5千米到達B景區,然后又回頭向西走8.5千米到達C景區,最后回到景區大門.
![]()
(1)以景區大門為原點,向東為正方向,以1個單位長表示1千米,建立如圖所示的數軸,請在數軸上表示出上述A、B、C三個景區的位置.
(2)A景區與C景區之間的距離是多少?
(3)若電瓶車充足一次電能行走15千米,則該電瓶車能否在一開始充足電而途中不充電的情況下完成此次任務?請計算說明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com