
【題目】如圖,E,F分別是 □ABCD的邊AB,CD的中點,則圖中平行四邊形的個數共有( ).
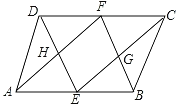
A. 2個 B. 3個 C. 4個 D. 5個
【答案】C
【解析】
首先根據四邊形ABCD是平行四邊形,可得DC∥AB,DC=AB,再根據E、F分別是邊AB、CD的中點,可得DF=FC=![]() DC,AE=EB=
DC,AE=EB=![]() AB,進而可根據一組對邊平行且相等的四邊形是平行四邊形證明四邊形DFBE和CFAE都是平行四邊形,再根據平行四邊形的性質可得DE∥FB,AF∥CE,進而可證出四邊形FHEG是平行四邊形。
AB,進而可根據一組對邊平行且相等的四邊形是平行四邊形證明四邊形DFBE和CFAE都是平行四邊形,再根據平行四邊形的性質可得DE∥FB,AF∥CE,進而可證出四邊形FHEG是平行四邊形。
解:∵四邊形ABCD是平行四邊形,
 ∴DC∥AB,DC=AB,
∴DC∥AB,DC=AB,
∵E、F分別是邊AB、CD的中點,
∴DF=FC=![]() DC,AE=EB=
DC,AE=EB=![]() AB,
AB,
∵DC=AB,
∴DF=FC=AE=EB,
∴四邊形DFBE和CFAE都是平行四邊形,
∴DE∥FB,AF∥CE,
∴四邊形FHEG是平行四邊形,
故選C。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】將一次函數y=kx+4(k≠0)的圖象稱為直線l.
(1)若直線l經過點(2,0),直接寫出關于x的不等式kx+4>0的解集;
(2)若直線l經過點(3,﹣2),求這個函數的表達式;
(3)若將直線l向右平移2個單位長度后經過點(5,5),求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是O的直徑,AE交O于點E,且與O的切線CD互相垂直,垂足為D. 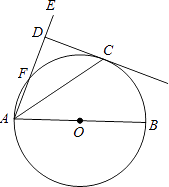
(1)求證:∠EAC=∠CAB;
(2)若CD=4,AD=8:①求O的半徑;②求tan∠BAE的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在今年法國網球公開賽中,我國選手李娜在決賽中成功擊敗對手奪冠,稱為獲得法國網球公開賽冠軍的亞洲第一人.某班體育委員就本班同學對該屆法國網球公開賽的了解程度進行全面調查統計,收集數據后繪制了兩幅不完整的統計圖,如圖(1)和圖(2).根據圖中的信息,解答下列問題: 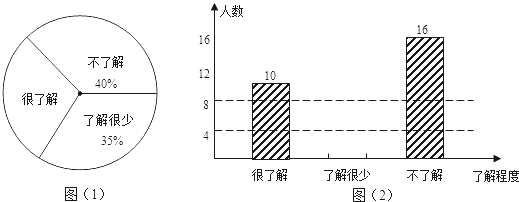
(1)該班共有名學生;
(2)在圖(1)中,“很了解”所對應的圓心角的度數為;
(3)把圖(2)中的條形圖形補充完整.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
在數學課上,老師提出如下問題:
已知:如圖,△ABC及AC邊的中點O。
求作:平行四邊形ABCD。
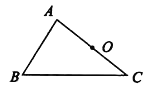
小敏的作法如下:
①連接BO并延長,在延長線上截取OD=BO;
②連接DA,DC.
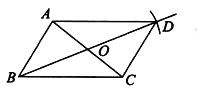
所以四邊形ABCD就是所求作的平行四邊形.
老師說:“小敏的作法正確.”
請回答:小敏的作法正確的理由是_________________________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com