
【題目】如圖,已知拋物線y=ax2+bx+3(a≠0)經過點A(1,0)和點B(3,0),與y軸交于點C.
(1)求此拋物線的解析式;
(2)若點P是直線BC下方的拋物線上一動點(不點B,C重合),過點P作y軸的平行線交直線BC于點D,設點P的橫坐標為m.
①用含m的代數式表示線段PD的長.
②連接PB,PC,求△PBC的面積最大時點P的坐標.
(3)設拋物線的對稱軸與BC交于點E,點M是拋物線的對稱軸上一點,N為y軸上一點,是否存在這樣的點M和點N,使得以點C、E、M、N為頂點的四邊形是菱形?如果存在,請直接寫出點M的坐標;如果不存在,請說明理由.

【答案】(1)y=x2﹣4x+3;(2)①﹣m2+3m,②(![]() ,﹣
,﹣![]() );(3)存在,點M的坐標為(2,3),( 2,1﹣2
);(3)存在,點M的坐標為(2,3),( 2,1﹣2![]() )或(2,1+2
)或(2,1+2![]() )
)
【解析】
(1)根據已知拋物線y=ax2+bx+3(a≠0)經過點A(1,0)和點B(3,0)代入即可求解;
(2)①先確定直線BC解析式,根據過點P作y軸的平行線交直線BC于點D,即可用含m的帶上書表示出P和D的坐標進而求解;
②用含m的代數式表示出△PBC的面積,可得S是關于m的二次函數,即可求解;
(3)根據(1)中所得二次函數圖象和對稱軸先得點E的坐標即可寫出點三個位置的點M的坐標.
解:(1)∵拋物線y=ax2+bx+3(a≠0)經過點A(1,0)和點B(3,0),與y軸交于點C,
∴![]() ,
,
解得:![]() ;
;
∴拋物線解析式為:y=x2﹣4x+3;
(2)如圖:
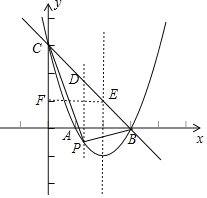
①設P(m,m2﹣4m+3),
將點B(3,0)、C(0,3)代入得直線BC解析式為yBC=﹣x+3.
∵過點P作y軸的平行線交直線BC于點D,
∴D(m,﹣m+3),
∴PD=(﹣m+3)﹣(m2﹣4m+3)=﹣m2+3m.
答:用含m的代數式表示線段PD的長為﹣m2+3m.
②S△PBC=S△CPD+S△BPD
=![]() OBPD=﹣
OBPD=﹣![]() m2+
m2+![]() m
m
=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() .
.
∴當m=![]() 時,S有最大值.
時,S有最大值.
當m=![]() 時,m2﹣4m+3=﹣
時,m2﹣4m+3=﹣![]() .
.
∴P(![]() ,﹣
,﹣![]() ).
).
答:△PBC的面積最大時點P的坐標為(![]() ,﹣
,﹣![]() ).
).
(3)存在這樣的點M和點N,使得以點C、E、M、N為頂點的四邊形是菱形.
根據題意,點E(2,1),
∴EF=CF=2,
∴EC=![]() ,
,
根據菱形的四條邊相等,
∴ME=EC=![]() ,
,
∴M(2,1﹣![]() )或(2,1+
)或(2,1+![]() )
)
當EM=EF=2時,M(2,3)
∴點M的坐標為M1(2,3),M2(2,1﹣2![]() ),M3(2,1+2
),M3(2,1+2![]() ).
).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面角坐標系xOy中,有一個等腰直角三角形△AOB,∠OAB=90°,直角邊AO在x軸上,且AO=1,將Rt△AOB繞原點O順時針旋轉90°后,再將各邊長擴大一倍,得到等腰直角三角形A1OB1;將Rt△A1OB1繞原點O順時針轉90°后,再將各邊長擴大一倍,得到等腰三角形A2OB2......依此規律,得到等腰直角三角形A2017OB2017,則點B2017的坐標_________ .
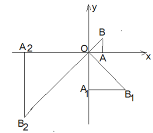
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】這是一個古老的傳說,講一個犯人利用概率來增加他得到寬恕的機會.給他兩個碗,一個里面裝著5個黑球,另一個里面裝著除顏色不同外其它都一樣的5個白球.把他的眼睛蒙著,然后要選擇一個碗,并從里面拿出一個球,如果他拿的是黑球就要繼續關在監獄里面,如果他拿的是白球,就將獲得自由.在蒙住眼睛之前允許他把球混合,重新分裝在兩個碗內(兩個碗球數可以不同).你能設想一下這個犯人怎么做,使得自己獲得自由的機會最大?則犯人獲得自由的最大機會是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了參加西部博覽會,資陽市計劃印制一批宣傳冊.該宣傳冊每本共10頁,由A、B兩種彩頁構成.已知A種彩頁制版費300元/張,B種彩頁制版費200元/張,共計2400元.(注:彩頁制版費與印數無關)
(1)每本宣傳冊A、B兩種彩頁各有多少張?
(2)據了解,A種彩頁印刷費2.5元/張,B種彩頁印刷費1.5元/張,這批宣傳冊的制版費與印刷費的和不超過30900元.如果按到資陽展臺處的參觀者人手一冊發放宣傳冊,預計最多能發給多少位參觀者?
查看答案和解析>>
科目:初中數學 來源: 題型:
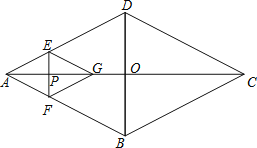
【題目】菱形ABCD的對角線AC,BD相交于點O,AC=16,BD=12,動點P在線段AC上從點A向點C以4個單位/秒的速度運動,過點P作EF⊥AC,交菱形ABCD的邊于點E、F,在直線AC上有一點G,使△AEF與△GEF關于EF對稱.設菱形ABCD被四邊形AEGF蓋住部分的面積為S1,未被蓋住部分的面積為S2,點P運動時間為x秒.
(1)用含x的代數式分別表示S1,S2;
(2)若S1=S2,求x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,![]() 中,
中,![]() 為
為![]() 內一點,將
內一點,將![]() 繞點
繞點![]() 按逆時針方向旋轉角
按逆時針方向旋轉角![]() 得到
得到![]() ,點
,點![]() 的對應點分別為點
的對應點分別為點![]() ,且
,且![]() 三點在同一直線上.
三點在同一直線上.
(1)填空:![]() (用含
(用含![]() 的代數式表示);
的代數式表示);
(2)如圖2,若![]() ,請補全圖形,再過點
,請補全圖形,再過點![]() 作
作![]() 于點
于點![]() ,然后探究線段
,然后探究線段![]() 之間的數量關系,并證明你的結論;
之間的數量關系,并證明你的結論;
(3)若![]() ,且點
,且點![]() 滿足
滿足![]() ,直接寫出點
,直接寫出點![]() 到
到![]() 的距離.
的距離.
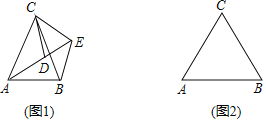
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形紙片ABCD中,AB=8,AD=17,折疊紙片使點B落在邊AD上的E處,折痕為PQ.當E在AD邊上移動時,折痕的端點P,Q也隨著移動.若限定P,Q分別在邊BA,BC上移動,則點E在邊AD上移動的最大距離為( )
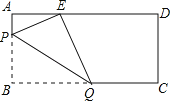
A.6B.7C.8D.9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,平面直角坐標系中,直線 y1=x+3與拋物線y2=﹣![]() +2x 的圖象如圖,點P是 y2 上的一個動點,則點P到直線 y1 的最短距離為()
+2x 的圖象如圖,點P是 y2 上的一個動點,則點P到直線 y1 的最短距離為()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠ACB=90°,AC=BC,點P在邊AB上,點D、Q分別為邊BC上的點,線段AD的延長線與線段PQ的延長線交于點F,連接CP交AF于點E,若∠BPF=∠APC,FD=FQ.
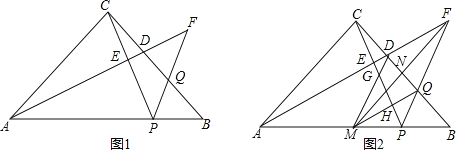
(1)如圖1,求證:AF⊥CP;
(2)如圖2,作∠AFP的平分線FM交AB于點M,交BC于點N,若FN=MN,求證:![]() ;
;
(3)在(2)的條件下,連接DM、MQ,分別交PC于點G、H,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com