【題目】在六張卡片上分別寫有 
，π，1.5，5，0， 
六個數，從中任意抽取一張，卡片上的數為無理數的概率是（ ）
A.
B.
C.
D.
【答案】B
【解析】解：∵六張卡片上分別寫有 
，π，1.5，5，0， 
六個數，無理數的是π， ，
∴從中任意抽取一張卡片上的數為無理數的概率是： ．
所以答案是：B．
【考點精析】本題主要考查了無理數和概率公式的相關知識點，需要掌握在理解無理數時，要抓住“無限不循環”這個要點，歸納起來有四類：（1）開方開不盡的數；（2）有特定意義的數，如圓周率π，或化簡后含有π的數；（3）有特定結構的數，如0.1010010001…等；（4）某些三角函數，如sin60o等；一般地，如果在一次試驗中，有n種可能的結果，并且它們發生的可能性都相等，事件A包含其中的m中結果，那么事件A發生的概率為P（A）=m/n才能正確解答此題．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】裝飾公司為小明家設計電視背景墻時需要A、B型板材若干塊，A型板材規格是ab，B型板材規格是bb．現只能購得規格是150b的標準板材．（單位：cm）
（1）若設a60cm，b30cm．一張標準板材盡可能多的裁出A型、B型板材，共有下表三種裁法，下圖是裁法一的裁剪示意圖．
裁法一 | 裁法二 | 裁法三 | |
A型板材塊數 | 1 | 2 | 0 |
B型板材塊數 | 3 | m | n |
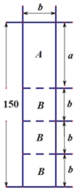
則上表中， m=___________， n=__________；
（2）為了裝修的需要，小明家又購買了若干C型板材，其規格是aa，并做成如下圖的背景墻．請寫出下圖中所表示的等式：__________；
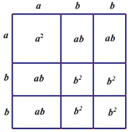
(3)若給定一個二次三項式2a25ab3b2，試用拼圖的方式將其因式分解．（請仿照（2）在幾何圖形中標上有關數量）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系
中，對于點
，若點
的坐標為
，則稱點是點
的“
演化點”.例如，點
的“
演化點”為
，即
.
（1）已知點
的“
演化點”是
，則的坐標為________；
（2）已知點
，且點
的“
演化點”是
，則
的面積
為__________；
（3）己知
，
，
，
，且點
的“
演化點”為
，當
時，
___________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形ABCD中，AB=4，BC=2，E是AB的中點，直線l平行于直線EC，且直線l與直線EC之間的距離為2，點F在矩形ABCD邊上，將矩形ABCD沿直線EF折疊，使點A恰好落在直線l上，則DF的長為 ．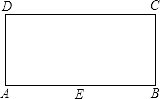 
查看答案和解析>>
科目：初中數學 來源： 題型：
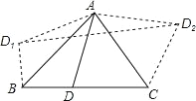
【題目】如圖，在△ABC中，∠ABC=45°，∠ACB=60°，BC=2
+2，D是BC邊上異于點B，C的一動點，將三角形ABD沿AB翻折得到△ABD1，將△ACD沿AC翻折得到△ACD2，連接D1D2，則四邊形D1BCD2的面積的最大值是_____.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，正方形A1B1C1O、A2B2C2B1、A3B3C3B2 ， …，按圖所示的方式放置．點A1、A2、A3 ， …和點B1、B2、B3 ， …分別在直線y=kx+b和x軸上．已知C1（1，﹣1），C2（ 
， 
），則點A3的坐標是 ．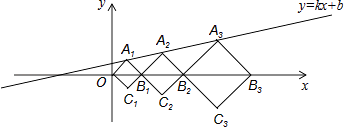 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】白色污染（ Whitepollution）是人們對難降解的塑料垃圾（多指塑料袋）污染環境現象的一種形象稱謂．為了讓全校同學感受丟棄塑料袋對環境的影響，小彬隨機抽取某小區
戶居民，記錄了這些家庭
年某個月丟棄塑料袋的數量（單位：個）
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
請根據上述數據，解答以下問題：
（1）小彬按“組距為
”列出了如下的頻數分布表（每組數據含最小值不含最大值），請將表中空缺的部分補充完整，并補全頻數直方圖；
分組 | 劃記 | 頻數 |
| _______ | ________ |
|
|
|
| _______ | ________ |
|
|
|
合計 | / |
|
（2）根據（1）中的直方圖可以看出，這戶居民家這個月丟棄塑料袋的個數在 組的家庭最多；（填分組序號）
（3）根據頻數分布表，小彬又畫出了如圖所示的扇形統計圖．請將統計圖中各組占總數的百分比填在圖中，并求出
組對應的扇形圓心角的度數；
（4）若該小區共有
戶居民家庭，請你估計每月丟棄的塑料袋數量不小于
個的家庭個數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平行四邊形ABCD中，點E為AD的中點，延長CE交BA的延長線于點F．
（1）求證：AB=AF；
（2）若BC=2AB，∠BCD=110°，求∠ABE的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知x2+（a+3）x+a+1=0是關于x的一元二次方程．
（1）求證：方程總有兩個不相等的實數根；
（2）若方程的兩個實數根為x1 ， x2 ， 且x12+x22=10，求實數a的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
