
如圖,現有兩塊全等的直角三角形紙板Ⅰ,Ⅱ,它們兩直角邊的長分別為1和2.將它們分別放置于平面直角坐標系中的 ,
, 處,直角邊
處,直角邊 在
在 軸上.一直尺從上方緊靠兩紙板放置,讓紙板Ⅰ沿直尺邊緣平行移動.當紙板Ⅰ移動至
軸上.一直尺從上方緊靠兩紙板放置,讓紙板Ⅰ沿直尺邊緣平行移動.當紙板Ⅰ移動至 處時,設
處時,設 與
與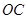 分別交于點
分別交于點 ,與
,與 軸分別交于點
軸分別交于點 .
.
(1)求直線 所對應的函數關系式;
所對應的函數關系式;
(2)當點 是線段
是線段 (端點除外)上的動點時,試探究:
(端點除外)上的動點時,試探究:
①點 到
到 軸的距離
軸的距離 與線段
與線段 的長是否總相等?請說明理由;
的長是否總相等?請說明理由;
②兩塊紙板重疊部分(圖中的陰影部分)的面積 是否存在最大值?若存在,求出這個最大值及
是否存在最大值?若存在,求出這個最大值及 取最大值時點
取最大值時點 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
(1)由直角三角形紙板的兩直角邊的長為1和2,
知 兩點的坐標分別為
兩點的坐標分別為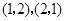 .
.
設直線 所對應的函數關系式為
所對應的函數關系式為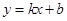 .
.
有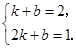 解得
解得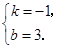
所以,直線 所對應的函數關系式為
所對應的函數關系式為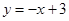 .
.
(2)①點 到
到 軸距離
軸距離 與線段
與線段 的長總相等.
的長總相等.
因為點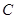 的坐標為
的坐標為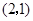 ,
,
所以,直線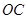 所對應的函數關系式為
所對應的函數關系式為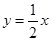 .
.
又因為點 在直線
在直線 上,
上,
所以可設點 的坐標為
的坐標為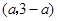 .
.
過點 作
作 軸的垂線,設垂足為點
軸的垂線,設垂足為點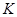 ,則有
,則有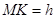 .
.
因為點 在直線
在直線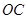 上,所以有
上,所以有 .
.
因為紙板為平行移動,故有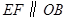 ,即
,即 .
.
又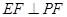 ,所以
,所以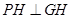 .
.
法一:故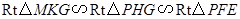 ,
,
從而有 .
.
得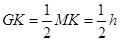 ,
,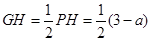 .
.
所以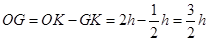 .
.
又有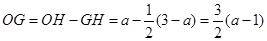 .
.
所以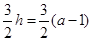 ,得
,得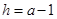 ,而
,而 ,
,
從而總有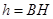 .
.
法二:故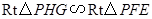 ,可得
,可得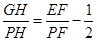 .
.
故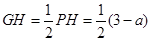 .
.
所以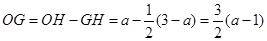 .
.
故 點坐標為
點坐標為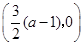 .
.
設直線 所對應的函數關系式為
所對應的函數關系式為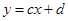 ,
,
則有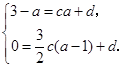 解得
解得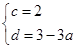
所以,直線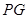 所對的函數關系式為
所對的函數關系式為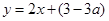 .
.
將點 的坐標代入,可得
的坐標代入,可得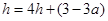 .解得
.解得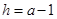 .
.
而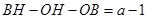 ,從而總有
,從而總有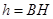 .
.
②由①知,點 的坐標為
的坐標為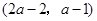 ,點
,點 的坐標為
的坐標為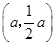 .
.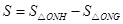
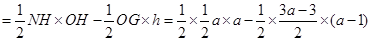
 .
.
當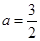 時,
時, 有最大值,最大值為
有最大值,最大值為 .
. 取最大值時點
取最大值時點 的坐標為
的坐標為 .
.
解析


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
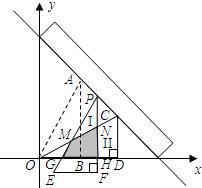 從上方緊靠兩紙板放置,讓紙板Ⅰ沿直尺邊緣平行移動.當紙板Ⅰ移動至△PEF處時,設PE,PF與OC分別交于點M,N,與x軸分別交于點G,H.
從上方緊靠兩紙板放置,讓紙板Ⅰ沿直尺邊緣平行移動.當紙板Ⅰ移動至△PEF處時,設PE,PF與OC分別交于點M,N,與x軸分別交于點G,H.查看答案和解析>>
科目:初中數學 來源:第2章《二次函數》常考題集(23):2.3 二次函數的應用(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:第26章《二次函數》中考題集(36):26.3 實際問題與二次函數(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2009年江蘇省中考數學仿真試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com