
【題目】如圖,已知拋物線y=﹣x2+bx+c與x軸交于A,B與y軸交于C,過C作x軸的平行線交拋物線于點D,過點D作x軸的垂線交x軸于E,點D的坐標為(2,3)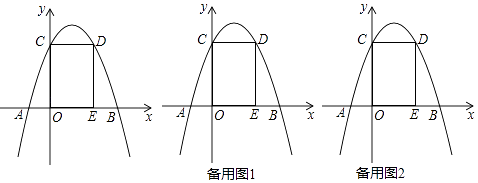
(1)求拋物線的解析式;
(2)點P為第一象限直線DE右側拋物線上一點,連接AP交y軸于點F,連接PD、DF,設點P的橫坐標為t,△PFD的面積為S,求S與t的函數關系式;
(3)在(2)的條件下,點P向下平移3個單位得到點Q,連接AQ、EQ,若∠AQE=45°,求點P的橫坐標.
【答案】
(1)解:由題意D(2,3),C(0,3),
∵CD∥x軸,
∴C、D關于對稱軸對稱,
∴對稱軸x=1,
∴﹣ ![]() =1,
=1,
∴b=2,c=3,
∴拋物線的解析式為y=﹣x2+2x+3.
(2)解:如圖1中,連接PC,作PH⊥AB于H.設P(t,﹣t2+2t+3).
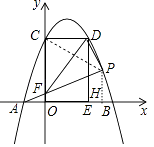
對于拋物線y=﹣x2+2x+3,令y=0,﹣x2+2x+3=0,解得x=﹣1或3,
∴A(﹣1,0),B(3,0)
∵OF∥PB,
∴ ![]() =
= ![]() ,
,
∴FO=(﹣t2+2t+3) ![]() =3﹣t,
=3﹣t,
∴CF=3﹣(3﹣t)=t,
S=S△PCF+S△PCD﹣S△CDF= ![]() tt+
tt+ ![]() ×2×[3﹣(﹣t2+2t+3)]﹣
×2×[3﹣(﹣t2+2t+3)]﹣ ![]() t2=
t2= ![]() t2﹣3t(2<t<3).
t2﹣3t(2<t<3).
(3)解:如圖構造等腰直角三角形△AKE,使得AK=EK,∠AKE=90°,則易知K( ![]() ,﹣
,﹣ ![]() ),以K為圓心,AK為半徑畫⊙K.
),以K為圓心,AK為半徑畫⊙K.
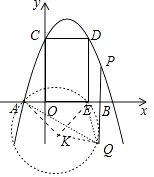
∵∠AQE=45°= ![]() ∠AKE,
∠AKE,
∴點Q在⊙K上,設P(m,﹣m2+2m+3),則Q(m,﹣m2+2m),
∵AK=QK,
∴(1+ ![]() )2+(
)2+( ![]() )2=(m﹣
)2=(m﹣ ![]() )2+(﹣m2+2m+
)2+(﹣m2+2m+ ![]() )2,
)2,
∴ ![]() +
+ ![]() =m2﹣m+
=m2﹣m+ ![]() +(﹣m2+2m)2+3(﹣m2+2m)+
+(﹣m2+2m)2+3(﹣m2+2m)+ ![]() ,
,
∴m2﹣m﹣2+m2(m﹣2)2﹣3m(m﹣2)=0,
∴(m﹣2)(m+1)+m2(m﹣2)2﹣3m(m﹣2)=0,
∴(m﹣2)[(m+1)+m3﹣2m2﹣3m]=0,
∴(m﹣2)[(m+1)+m(m+1)(m﹣3)]=0,
∴(m﹣2)(m+1)(m2
∴m=2或﹣1或 ![]() ,
,
∵點P為第一象限直線DE右側拋物線上一點,
∴m= ![]() ,
,
∴滿足條件的點P的橫坐標為 ![]() .
.
【解析】(1)根據題意易求得點C的坐標,再用待定系數法求出拋物線的解析式。或根據點C、D是兩對稱點,求出對稱軸,即可求出拋物線的解析式。
(2)觀察函數圖像,可知S△PFD=S△PCF+S△PCD﹣S△CDF,因此連接PC,作PH⊥AB于H.設P(t,﹣t2+2t+3),再用含t的代數式分別求出△PCF、△PCD、△CDF的面積,就可以求出S與t的函數關系式。
(3)抓住已知∠AQE=45°,添加輔助線,構造圓周角為45°的圓心角,構造等腰直角三角形△AKE,使得AK=EK,∠AKE=90°,以K為圓心,AK為半徑畫⊙K,易得到K點坐標,得出點Q在圓上,設出點P、點Q的坐標,根據AK=QK。列出方程,求解即可求出點P的橫坐標。
【考點精析】解答此題的關鍵在于理解勾股定理的概念的相關知識,掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2,以及對矩形的性質的理解,了解矩形的四個角都是直角,矩形的對角線相等.


 名牌中學課時作業系列答案
名牌中學課時作業系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案科目:初中數學 來源: 題型:
【題目】已知I是△ABC的內心,AI延長線交△ABC外接圓于D,連BD.
(1)在圖1中,求證:DB=DI;
(2)如圖2,若AB為直徑,且OI⊥AD于I點,DE切圓于D點,求sin∠ADE的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文教店老板到批發市場選購A,B兩種品牌的繪圖工具套裝,每套A品牌套裝進價比B品牌每套套裝進價多2.5元,已知用200元購進A種套裝的數量是用75元購進B種套裝數量的2倍.
(1)求A,B兩種品牌套裝每套進價分別為多少元?
(2)若A品牌套裝每套售價為13元,B品牌套裝每套售價為9.5元,店老板決定,購進B品牌的數量比購進A品牌的數量的2倍還多4套,兩種工具套裝全部售出后,要使總的獲利超過120元,則最少購進A品牌工具套裝多少套?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為評估九年級學生的學習成績狀況,以應對即將到來的中考做好教學調整,某中學抽取了部分參加考試的學生的成績作為樣本分析,繪制成了如下兩幅不完整的統計圖,請根據圖中提供的信息解答下列問題:
(1)求本中學成績類別為“中”的人數;
(2)求出扇形圖中,“優”所占的百分比,并將條形統計圖補充完整;
(3)該校九年級共有1000人參加了這次考試,請估算該校九年級共有多少名學生的數學成績達到優秀?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A、B兩村在一條小河的同一側,要在河邊建一水廠向兩村供水
(1)若要使自來水廠到兩村的距離相等,廠址應選在哪個位置?
(2)若要使自來水廠到兩村的輸水管用料最省,廠址應選在哪個位置?
請用尺規作圖,將上述兩種情況下的自來水廠廠址分別在圖(1)(2)中標出,并保留作圖痕跡。

查看答案和解析>>
科目:初中數學 來源: 題型:
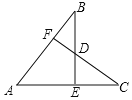
【題目】如圖,已知AB=AC,BE⊥AC于點E,CF⊥AB于點F,BE與CF交于點D,則下列結論中不正確的是( )
A. ![]() B.
B. ![]() C. 點D在
C. 點D在![]() 的平分線上D. 點D是CF的中點
的平分線上D. 點D是CF的中點
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】便民服裝店的老板在株洲看到一種夏季襯衫,就用8000元購進若干件,以每件58元的價格出售,很快售完,又用17600元購進同種襯衫,數量是第一次的2倍每件進價比第一次多了4元,服裝店仍按每件58元出售,全部售完,問該服裝店兩次一共盈利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1是一個長為2m、寬為2n的長方形,沿圖中虛線用剪刀均分成四塊小長方形,然后按圖2的形狀拼成一個正方形.
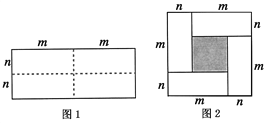
(1)請用兩種不同的方法求圖2中陰影部分的面積.
方法1: ;
方法2: ;
(2)觀察圖2請你寫出下列三個代數式:(m+n)2,(m-n)2,mn之間的等量關系 ;
(3)根據(2)題中的等量關系,解決如下問題:
①已知:![]() ,
,![]() ,求:
,求:![]() 的值;
的值;
②已知:![]() ,
,![]() ,求:
,求:![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com