【題目】某養殖戶的養殖成本逐年增長，已知第一年的養殖成本為12萬元，第3年的養殖成本為17萬元．設每年平均增長的百分率為x，則下面所列方程中正確的是（ ）
A.12（1﹣x）2=17
B.17（1﹣x）2=12
C.17（1+x）2=12
D.12（1+x）2=17
期末沖刺100分創新金卷完全試卷系列答案科目：初中數學 來源： 題型：
【題目】已知：如圖①，在矩形ABCD中，AB=5，AD=
，AE⊥BD，垂足是E．點F是點E關于AB的對稱點，連接AF、BF．
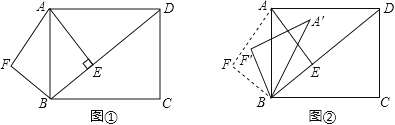
（1）求AE和BE的長；
（2）若將△ABF沿著射線BD方向平移，設平移的距離為m（平移距離指點B沿BD方向所經過的線段長度）．當點F分別平移到線段AB、AD上時，直接寫出相應的m的值．
（3）如圖②，將△ABF繞點B順時針旋轉一個角α（0°＜α＜180°），記旋轉中的△ABF為△A′BF′，在旋轉過程中，設A′F′所在的直線與直線AD交于點P，與直線BD交于點Q．是否存在這樣的P、Q兩點，使△DPQ為等腰三角形？若存在，求出此時DQ的長；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】把拋物線y=-x2+2的圖象繞原點旋轉180°，所得的拋物線的函數關系是( )
A. y=x2+2B. y=-x2+2C. y=-x2-2D. y=x2-2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某農場去年種植了10畝地的南瓜，畝產量為2000kg，根據市場需要，今年該農場擴大了種植面積，并且全部種植了高產的新品種南瓜，已知南瓜種植面積的增長率是畝產量的增長率的2倍，今年南瓜的總產量為60000kg，求南瓜畝產量的增長率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用配方法解方程x2﹣2x﹣2＝0，原方程應變形為( )
A. (x+1)2＝3B. (x﹣1)2＝3C. (x+1)2＝1D. (x﹣1)2＝1
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某區教育局為了解今年九年級學生體育測試情況，隨機抽查了某班學生的體育測試成績為樣本，按A、B、C、D四個等級進行統計，并將統計結果繪制成如下的統計圖，請你結合圖中所給信息解答下列問題：
說明：A級：90分～100分；B級：75分～89分；C級：60分～74分；D級：60分以下
（1）樣本中D級的學生人數占全班學生人數的百分比是 ；
（2）扇形統計圖中A級所在的扇形的圓心角度數是 ；
（3）請把條形統計圖補充完整；
（4）若該校九年級有500名學生，請你用此樣本估計體育測試中A級和B級的學生人數之和．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在□ABCD中，點E、F分別是AD、BC的中點，分別連接BE、DF、BD．
（1）求證：△AEB≌△CFD；
（2）若四邊形EBFD是菱形，求∠ABD的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ACB為直角，AB=10，
°，半徑為1的動圓Q的圓心從點C出發，沿著CB方向以1個單位長度/秒的速度勻速運動，同時動點P從點B出發，沿著BA方向也以1個單位長度/秒的速度勻速運動，設運動時間為t秒（0＜t≤5）以P為圓心，PB長為半徑的⊙P與AB、BC的另一個交點分別為E、D，連結ED、EQ．
（1）判斷并證明ED與BC的位置關系，并求當點Q與點D重合時t的值；
（2）當⊙P和AC相交時，設CQ為
，⊙P被AC 截得的弦長為
，求關于的函數； 并求當⊙Q過點B時⊙P被AC截得的弦長；
（3）若⊙P與⊙Q相交，寫出t的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
