
【題目】如圖,直線![]() 的函數解析式為
的函數解析式為![]() ,且
,且![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 經過點
經過點![]() 、
、![]() ,直線
,直線![]() 、
、![]() 交于點
交于點![]() .
.
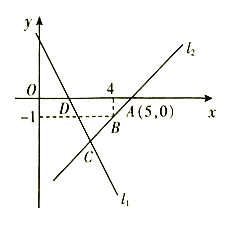
(1)求直線![]() 的函數解析式;
的函數解析式;
(2)求![]() 的面積;
的面積;
(3)在直線![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 面積是
面積是![]() 面積的
面積的![]() 倍?如果存在,請求出
倍?如果存在,請求出![]() 坐標;如果不存在,請說明理由.
坐標;如果不存在,請說明理由.
【答案】(1)![]() ;(2)3;(3)在直線
;(2)3;(3)在直線![]() 上存在點
上存在點![]() 或
或![]() ,使得
,使得![]() 面積是
面積是![]() 面積的
面積的![]() 倍.
倍.
【解析】
(1)根據點A、B的坐標利用待定系數法即可求出直線l2的函數解析式;
(2)令y=-2x+4=0求出x值,即可得出點D的坐標,聯立兩直線解析式成方程組,解方程組即可得出點C的坐標,再根據三角形的面積即可得出結論;
(3)假設存在點P,使得△ADP面積是△ADC面積的1.5倍,根據兩三角形面積間的關系|yP|=1.5|yC|=3,再根據一次函數圖象上點的坐標特征即可求出點P的坐標.
解:(1)設直線![]() 的函數解析式為
的函數解析式為![]() ,
,
將![]() 、
、![]() 代入
代入![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() 直線
直線![]() 的函數解析式為
的函數解析式為![]() .
.
(2)聯立兩直線解析式成方程組,
![]() ,解得:
,解得:![]() ,
,
![]() 點
點![]() 的坐標為
的坐標為![]() .
.
當![]() 時,
時,![]() ,
,
![]() 點
點![]() 的坐標為
的坐標為![]() .
.
![]() .
.
(3)假設存在.
![]() 面積是
面積是![]() 面積的
面積的![]() 倍,
倍,
![]() ,
,
當![]() 時,
時,![]() ,
,
此時點![]() 的坐標為
的坐標為![]() ;
;
當![]() 時,
時,![]() ,
,
此時點![]() 的坐標為
的坐標為![]() .
.
綜上所述:在直線![]() 上存在點
上存在點![]() 或
或![]() ,使得
,使得![]() 面積是
面積是![]() 面積的
面積的![]() 倍.
倍.
故答案為:(1)![]() ;(2)3;(3)在直線
;(2)3;(3)在直線![]() 上存在點
上存在點![]() 或
或![]() ,使得
,使得![]() 面積是
面積是![]() 面積的
面積的![]() 倍.
倍.


科目:初中數學 來源: 題型:
【題目】被歷代數學家尊為“算經之首”的《九章算術》是中國古代算法的扛鼎之作.《九章算術》中記載:“今有五雀、六燕,集稱之衡,雀俱重,燕俱輕.一雀一燕交而處,衡適平.并燕、雀重一斤.問燕、雀一枚各重幾何?”
譯文:“今有5只雀、6只燕,分別聚集而且用衡器稱之,聚在一起的雀重,燕輕.將一只雀、一只燕交換位置而放,重量相等.5只雀、6只燕重量為1斤.問雀、燕毎只各重多少斤?”
設每只雀重x斤,每只燕重y斤,可列方程組為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
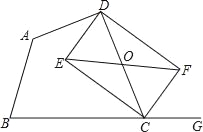
【題目】已知:如圖,在四邊形ABCD中,點G在邊BC的延長線上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于點O.
(1)求證:OE=OF;
(2)若點O為CD的中點,求證:四邊形DECF是矩形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 年
年![]() 月
月![]() 日是第
日是第![]() 個世界讀書日,為迎接第
個世界讀書日,為迎接第![]() 個世界讀書日的到來,某校舉辦讀書分享大賽活動:大賽以“推薦分享”為主題,參賽者選擇一本自己最喜歡的書,然后給該書寫一段推薦語、一篇讀書心得、舉辦一場讀書講座.大賽組委會對參賽者提交的推薦語、讀書心得、舉辦的讀書講座進行打分(各項成績均按百分制),綜合成績排名第一的選手將獲得大賽一等獎.現有甲、乙兩位同學的各項成績如下表所示;
個世界讀書日的到來,某校舉辦讀書分享大賽活動:大賽以“推薦分享”為主題,參賽者選擇一本自己最喜歡的書,然后給該書寫一段推薦語、一篇讀書心得、舉辦一場讀書講座.大賽組委會對參賽者提交的推薦語、讀書心得、舉辦的讀書講座進行打分(各項成績均按百分制),綜合成績排名第一的選手將獲得大賽一等獎.現有甲、乙兩位同學的各項成績如下表所示;
參賽者 | 推薦語 | 讀書心得 | 讀書講座 |
甲 |
|
|
|
乙 |
|
|
|
(1)若將三項成績的平均分作為參賽選手的綜合成績,則甲、乙二人誰最有可能獲得大賽一等獎?請通過計算說明理由.
(2)若“推薦語”“讀書心得”“讀書講座”的成績按![]() 確定綜合成績,則甲、乙二人誰最有可能獲得大賽一等獎?請通過計算說明理由.
確定綜合成績,則甲、乙二人誰最有可能獲得大賽一等獎?請通過計算說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數軸上點A表示整數a,且![]() ,點B表示a的相反數.
,點B表示a的相反數.
(1)畫數軸,并在數軸上標出點A與點B;
(2)點P, Q 在線段AB上,且點P在點Q的左側,若P, Q兩點沿數軸相向勻速運動,出發后經4秒兩點相遇. 已知在相遇時點Q比點P多行駛了3個單位,相遇后經1秒點Q到達點P的起始位置. 問點P、Q運動的速度分別是每秒多少個單位;.
(3)在(2)的條件下,若點P從整數點出發,當運動時間為t秒時(t是整數),將數軸折疊,使A點與B點重合,經過折疊P點與Q點也恰好重合,求P點的起始位置表示的數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,將
,將![]() 繞點A按順時針方向旋轉得到
繞點A按順時針方向旋轉得到![]() 旋轉角為
旋轉角為![]() ,點B,點C的對應點分別為點D,點E,過點D作直線AB的垂線,垂足為F,過點E作直線AC的垂線,垂足為P,當
,點B,點C的對應點分別為點D,點E,過點D作直線AB的垂線,垂足為F,過點E作直線AC的垂線,垂足為P,當![]() 時,點P與點C之間的距離是________.
時,點P與點C之間的距離是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位計劃在暑假陰間組織員工到某地旅游,參加旅游的人數估計為10~25人,甲、乙兩家旅行社的服務質量相同,且報價都是每人200元.經過協商,甲旅行社表示可給予每位游客七折優惠;乙旅行社表示可先免去一位游客的費用,其余游客七五折優惠.設該單位參加旅游的人數是x人.選擇甲旅行社時,所需費用為![]() 元,選擇乙旅行社時,所需費用為
元,選擇乙旅行社時,所需費用為![]() 元.
元.
(1)寫出甲旅行社收費![]() (元)與參加旅游的人數x(人)之間的關系式.
(元)與參加旅游的人數x(人)之間的關系式.
(2)寫出乙旅行社收費![]() (元)與參加旅游的人數x(人)之間的關系式.
(元)與參加旅游的人數x(人)之間的關系式.
(3)該單位選擇哪一家旅行社支付的旅游費用較少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,菱形ABOC的頂點O在坐標原點,邊BO在x軸的負半軸上,![]() ,頂點C的坐標為
,頂點C的坐標為![]() ,x反比例函數
,x反比例函數![]() 的圖象與菱形對角線AO交于點D,連接BD,當
的圖象與菱形對角線AO交于點D,連接BD,當![]() 軸時,k的值是______.
軸時,k的值是______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com