【題目】閱讀下面材料：
在數學課上，老師提出如下問題：
已知:如圖，四邊形ABCD是平行四邊形
求作：菱形AECF，使E，F分別在BC，AAD上
小凱的作法如下：
⑴連接AC
⑵作AC的垂直平分線EF分別交BC，AD于E，F
⑶連接AE，CF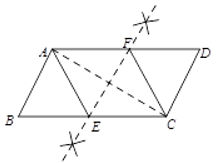
所以四邊形AECF是菱形
老師說：“小凱的作法正確．”
請回答：在小凱的作法中，判定四邊形AECF是菱形的依據是
【答案】對角線互相垂直的平行四邊形是菱形．（或有一組鄰邊相等的平行四邊形是菱形．或四條邊都相等的四邊形是菱形．）
【解析】解：答案為對角線互相垂直的平行四邊形是菱形或有一組鄰邊相等的平行四邊形是菱形或四條邊都相等的四邊形是菱形.由作法得EF垂直平分AC、則FA=FC，EA=EC，再證明四邊形AECF為平行四邊形，從而得到四邊形AECF為菱形.
【考點精析】關于本題考查的平行四邊形的判定和菱形的判定方法，需要了解兩組對邊分別平行的四邊形是平行四邊形：兩組對邊分別相等的四邊形是平行四邊形；一組對邊平行且相等的四邊形是平行四邊形；兩組對角分別相等的四邊形是平行四邊形；對角線互相平分的四邊形是平行四邊形；任意一個四邊形，四邊相等成菱形；四邊形的對角線，垂直互分是菱形．已知平行四邊形，鄰邊相等叫菱形；兩對角線若垂直，順理成章為菱形才能得出正確答案．
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】下列說法中，正確的是( )
A. 兩條不相交的直線叫做平行線
B. 一條直線的平行線有且只有一條
C. 若直線a∥b，a∥c，則b∥c
D. 若兩條線段不相交，則它們互相平行
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線y=kx+b與雙曲線
（x﹤0）相交于A（-4，a）、B（-1，4）兩點.
（1）求直線和雙曲線的解析式；
（2）在y軸上存在一點P，使得PA+PB的值最小，求點P的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，⊙O是△ABC的外接圓，AB是⊙O的直徑，FO⊥AB，垂足為點O，連接AF并延長交⊙O于點D，連接OD交BC于點E，∠B=30°，FO=2
．
（1）求AC的長度；
（2）求圖中陰影部分的面積．（計算結果保留根號）
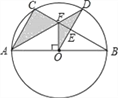
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】麻城市思源實驗學校自從開展“高效課堂”模式以來，在課堂上進行當堂檢測效果很好．每節課40分鐘教學，假設老師用于精講的時間x（單位：分鐘）與學生學習收益量y的關系如圖1所示，學生用于當堂檢測的時間x（單位：分鐘）與學生學習收益y的關系如圖2所示（其中OA是拋物線的一部分，A為拋物線的頂點），且用于當堂檢測的時間不超過用于精講的時間．
（1）求老師精講時的學生學習收益量y與用于精講的時間x之間的函數關系式；
（2）求學生當堂檢測的學習收益量y與用于當堂檢測的時間x的函數關系式；
（3）問此“高效課堂”模式如何分配精講和當堂檢測的時間，才能使學生在這40分鐘的學習收益總量最大？
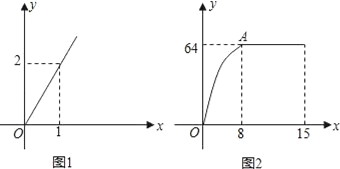
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列有關圓的一些結論：①與半徑長相等的弦所對的圓周角是30°；②圓內接正六邊形的邊長與該圓半徑相等；③垂直于弦的直徑平分這條弦；④平分弦的直徑垂直于弦．其中正確的是（ ）
A.①②③
B.①③④
C.②③
D.②④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于正數 
，用符號 
表示 的整數部分，例如： 
， 
， 
．點 
在第一象限內，以A為對角線的交點畫一個矩形，使它的邊分別與兩坐標軸垂直. 其中垂直于 
軸的邊長為 
，垂直于 軸的邊長為 
，那么，把這個矩形覆蓋的區域叫做點A的矩形域．例如：點 
的矩形域是一個以 為對角線交點，長為3，寬為2的矩形所覆蓋的區域，如圖1所示，它的面積是6．
圖1 圖2
根據上面的定義，回答下列問題：
（1）在圖2所示的坐標系中畫出點 的矩形域，該矩形域的面積是；
（2）點 
的矩形域重疊部分面積為1，求 的值；
（3）已知點 
在直線 
上， 且點B的矩形域的面積 
滿足 
，那么 
的取值范圍是 ． （直接寫出結果）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
