
【題目】如圖所示,已知![]() 的直徑
的直徑![]() ,延長(zhǎng)
,延長(zhǎng)![]() 到
到![]() ,使
,使![]() ,過
,過![]() 作
作![]() 的切線
的切線![]() ,
,![]() 為切點(diǎn),連接
為切點(diǎn),連接![]() 、
、![]() .求:
.求:

![]() 的長(zhǎng);
的長(zhǎng);
![]() 的值;
的值;
![]() 的面積.
的面積.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)連結(jié)OD,根據(jù)切線的性質(zhì)得OD⊥DC,由于BC=AB=1得到OD=![]() ,OC=
,OC=![]() ,在
,在![]() 中,根據(jù)勾股定理即可求得DC=
中,根據(jù)勾股定理即可求得DC=![]() ;(2)根據(jù)已知條件易證△CDB∽△CAD,根據(jù)相似三角形的性質(zhì)可得DB:DA=CD:CA=
;(2)根據(jù)已知條件易證△CDB∽△CAD,根據(jù)相似三角形的性質(zhì)可得DB:DA=CD:CA=![]() :2,由此即可求得AD:BD的值;(3設(shè)DB=x,則AD=
:2,由此即可求得AD:BD的值;(3設(shè)DB=x,則AD=![]() x,在Rt△ADB中,根據(jù)勾股定理可得方程
x,在Rt△ADB中,根據(jù)勾股定理可得方程![]() ,解得x=
,解得x=![]() ,即可得DB
,即可得DB![]() ,
,![]() ,然后根據(jù)三角形面積公式即可求得△ABD的面積.
,然后根據(jù)三角形面積公式即可求得△ABD的面積.
![]() 連結(jié)
連結(jié)![]() ,如圖,
,如圖,

∵![]() 為
為![]() 的切線,
的切線,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ;
;
![]() ∵
∵![]() ,
,
而![]() ,
,
∴![]() ,
,
∵![]() 為直徑,
為直徑,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
而![]() 公共,
公共,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 設(shè)
設(shè)![]() ,則
,則![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 的面積
的面積![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
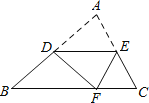
【題目】如圖,在△ABC中,∠A=70°∠B=50°,點(diǎn)D,E分別為AB,AC上的點(diǎn),沿DE折疊,使點(diǎn)A落在BC邊上點(diǎn)F處,若△EFC為直角三角形,則∠BDF的度數(shù)為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:在△ABC中,∠ACB=90°,點(diǎn)P是線段AC上一點(diǎn),過點(diǎn)A作AB的垂線,交BP的延長(zhǎng)線于點(diǎn)M,MN⊥AC于點(diǎn)N,PQ⊥AB于點(diǎn)Q,AQ=MN. 求證:
(1)△APM是等腰三角形;
(2)PC=AN.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
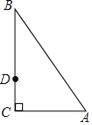
【題目】如圖,在△ABC中,∠C=90°,∠A=60°,點(diǎn)E,F(xiàn)分別在AB,AC上,把∠A沿著EF對(duì)折,使點(diǎn)A落在BC上的點(diǎn)D處.
(1)用尺規(guī)作圖的方法,在圖中找出點(diǎn)E,F(xiàn)的位置,并連接DE,DF(保留作圖痕跡,不要求寫作法);
(2)若ED⊥BC,求證:四邊形AEDF是菱形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在平面直角坐標(biāo)系xOy中,點(diǎn)A的坐標(biāo)為(4,0),以點(diǎn)A為圓心,4為半徑的圓與x軸交于O,B兩點(diǎn),OC為弦,∠AOC=60°,P是x軸上的一動(dòng)點(diǎn),連接CP.
(1)直接寫出OC=___________;
(2)如圖1,當(dāng)CP與⊙A相切時(shí),求PO的長(zhǎng);
(3)如圖2,當(dāng)點(diǎn)P在直徑OB上時(shí),CP的延長(zhǎng)線與⊙A相交于點(diǎn)Q,問當(dāng)PO為何值時(shí),△OCQ是等腰三角形?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在四邊形ABCD中,AB∥CD,AD//BC,點(diǎn)E,F在對(duì)角線AC上,且AE=CF,請(qǐng)你分別以E,F為一端點(diǎn),和圖中已標(biāo)字母的某點(diǎn)連成兩條相等的新線段(只需證明一組線段相等即可).
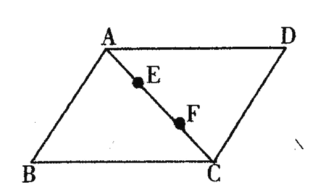
(1)連接 ;
(2)結(jié)論: = ;
(3)證明:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=AD,對(duì)角線AC,BD交于點(diǎn)E,點(diǎn)O在線段AE上,⊙O過B,D兩點(diǎn),若OC=5,OB=3,且cos∠BOE=![]() .求證:CB是⊙O的切線.
.求證:CB是⊙O的切線.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在大同市開張的美化城市活動(dòng)中,某居民小區(qū)要在一塊一邊靠墻(墻長(zhǎng)![]() )的空地上修建一個(gè)矩形花園
)的空地上修建一個(gè)矩形花園![]() ,花園的一邊靠前,另三邊用總長(zhǎng)為
,花園的一邊靠前,另三邊用總長(zhǎng)為![]() 的柵欄圍成(如圖所示),若設(shè)花園的
的柵欄圍成(如圖所示),若設(shè)花園的![]() 長(zhǎng)為
長(zhǎng)為![]() ,花園的面積為
,花園的面積為![]() .
.
![]() 求
求![]() 與
與![]() 之間的函數(shù)關(guān)系式,并寫出自變量的取值范圍;
之間的函數(shù)關(guān)系式,并寫出自變量的取值范圍;
![]() 滿足條件的花園面積能達(dá)到
滿足條件的花園面積能達(dá)到![]() 嗎?若能,求出此時(shí)
嗎?若能,求出此時(shí)![]() 的值;若不能,說明理由;
的值;若不能,說明理由;
![]() 根據(jù)
根據(jù)![]() 中求得的函數(shù)關(guān)系式,描述其圖象的變化趨勢(shì);并結(jié)合題意判斷當(dāng)
中求得的函數(shù)關(guān)系式,描述其圖象的變化趨勢(shì);并結(jié)合題意判斷當(dāng)![]() 取何值時(shí),花園的面積最大?最大面積為多少?
取何值時(shí),花園的面積最大?最大面積為多少?
![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,AC=BC=AD.

(1)作∠A的平分線交CD于E;
(2)過B作CD的垂線,垂足為F;
(3)請(qǐng)寫出圖中兩對(duì)全等三角形(不添加任何字母),并選擇其中一對(duì)加以證明.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com