
【題目】如圖,△![]() 是等邊三角形,
是等邊三角形, ![]() =2
=2![]() .點
.點![]() 從點
從點![]() 出發沿沿射線
出發沿沿射線![]() 以1
以1 ![]() 的速度運動,過點
的速度運動,過點![]() 作
作![]() ∥
∥![]() 交射線
交射線![]() 于點
于點![]() ,同時點
,同時點![]() 從點
從點![]() 出發沿
出發沿![]() 的延長線以1
的延長線以1 ![]() 的速度運動,連結
的速度運動,連結![]() 、
、![]() .設點
.設點![]() 的運動時間我
的運動時間我![]() (
(![]() ).
).
(1)求證:△![]() 是等邊三角形;
是等邊三角形;
(2)直接寫出![]() 的長(用含
的長(用含![]() 的代數式表示);
的代數式表示);
(3)當點![]() 在邊
在邊![]() 上,且不與點
上,且不與點![]() 、
、![]() 重合時,求證:△
重合時,求證:△![]() ≌△
≌△![]() .
.
(4)在不添加字母和連結其它線段的條件下,當圖中等腰三角形的個數大于3時,直接寫出t的值和對應的等腰三角形的個數.

【答案】(1)證明見解析;
(2)![]() 或
或![]() ;
;
(3)證明見解析;
(4)當t=1時,圖中有5個等腰三角形,當t=4時,圖中有4個等腰三角形.
【解析】【試題分析】
(1)△ABC是等邊三角形,根據等邊三角形的定義得:∠A=∠ABC=60°.
由于![]() ,根據兩直線平行,同位角相等得:∠APE=∠ABC=60°.
,根據兩直線平行,同位角相等得:∠APE=∠ABC=60°.
因為∠A=∠APE=60°.根據等邊三角形的判定得:△APE是等邊三角形.
(2)由題意得:AE=AP=t,當t<2時,CE= ![]() ;當t>2時,CE=
;當t>2時,CE= ![]() .
. ![]() 或
或![]() .
.
(3)根據△ABC是等邊三角形,得到,AB=AC,∠ACB=60°.因為△APE是等邊三角形,
得AP=PE=AE,∠APE=60°.則AB-AP=AC-AE,∠BPE=∠ECQ=120°.根據等量相減仍是等量得:BP=EC.由于AP=CQ=t,所以PE=CQ.根據SAS得,△BPE≌ECQ.
(4)當t=1時,圖中有5個等腰三角形. ![]()
當t=4時,如圖,圖中有4個等腰三角形. ![]()
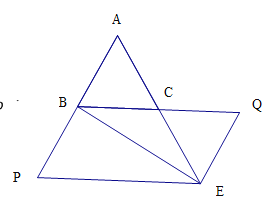
【試題解析】
(1)∵△ABC是等邊三角形,
∴∠A=∠ABC=60°.
∵![]() ,
,
∴∠APE=∠ABC=60°.
∴∠A=∠APE=60°.
∴△APE是等邊三角形.
(2)當t<2時,CE= ![]() ;當t>2時,CE=
;當t>2時,CE= ![]() .
.
(3)∵△ABC是等邊三角形,
∴AB=AC,∠ACB=60°.
∵△APE是等邊三角形,
∴AP=PE=AE,∠APE=60°.
∴AB-AP=AC-AE,∠BPE=∠ECQ=120°.
∴BP=EC.
∵AP=CQ=t,
∴PE=CQ.
∴△BPE≌ECQ.
(4)當t=1時,圖中有5個等腰三角形.
當t=4時,如圖,圖中有4個等腰三角形.



科目:初中數學 來源: 題型:
【題目】如圖所示,△ABO中,A,B兩點的坐標分別為(2,4),(7,2),C,G,F,E分別為過A,B兩點所作的y軸、x軸的垂線與y軸、x軸的交點.求△AOB的面積.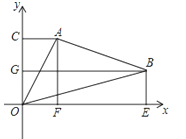
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年3月份某省農產品實現出口額8 3620000美元.其中8 3620000用科學記數法表示為( )
A.8.362×107
B.83.62×106
C.0.8362×108
D.8.362×108
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】南山植物園中現有A、B兩個園區,已知A園區為長方形,長為(x+y)米,寬為(x﹣y)米;B園區為正方形,邊長為(x+3y)米.
(1)請用代數式表示A、B兩園區的面積之和并化簡;
(2)現根據實際需要對A園區進行整改,長增加(11x﹣y)米,寬減少(x﹣2y)米,整改后A區的長比寬多350米,且整改后兩園區的周長之和為980米.
①求x、y的值;
②若A園區全部種植C種花,B園區全部種植D種花,且C、D兩種花投入的費用與吸引游客的收益如表:
C | D | |
投入(元/平方米) | 12 | 16 |
收益(元/平方米) | 18 | 26 |
求整改后A、B兩園區旅游的凈收益之和.(凈收益=收益﹣投入)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,拋物線y=![]() 與直線y=﹣
與直線y=﹣![]() x﹣
x﹣![]() 交于A、B兩點,已知點B的橫坐標是4,直線y=﹣
交于A、B兩點,已知點B的橫坐標是4,直線y=﹣![]() x﹣
x﹣![]() 與x、y軸的交點分別為A、C,點P是拋物線上一動點.
與x、y軸的交點分別為A、C,點P是拋物線上一動點.

(1)求拋物線的解析式;
(2)若點P在直線y=﹣![]() x﹣
x﹣![]() 上方,求△PAC的最大面積;
上方,求△PAC的最大面積;
(3)設M是拋物線對稱軸上的一點,以點A、B、P、M為頂點的四邊形能否成為平行四邊形?若能,求出點P的坐標;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com