
【題目】聯(lián)想三角形外心的概念,我們可引入如下概念:到三角形的兩個頂點距離相等的點,叫做此三角形的準外心.例:已知![]() ,則點
,則點![]() 為
為![]() 的準外心(如圖
的準外心(如圖![]() ).
).
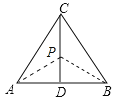
![]() 如圖
如圖![]() ,
,![]() 為正三角形
為正三角形![]() 的高,準外心
的高,準外心![]() 在高
在高![]() 上,且
上,且![]() ,求
,求![]() 的度數(shù).
的度數(shù).
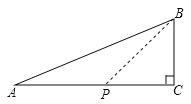
![]() 如圖
如圖![]() ,若
,若![]() 為直角三角形,
為直角三角形,![]() ,
,![]() ,
,![]() ,準外心
,準外心![]() 在
在![]() 邊上,試探究
邊上,試探究![]() 的長.
的長.



【答案】∠APB=90°;(2)PA=![]() 或6.
或6.
【解析】
(1)利用分類討論:①若PB=PC,②若PA=PC,③若PA=PB,進而求出即可;
(2)利用分類討論:①若PB=PA,②若PA=PC,③若PC=PB,進而求出即可.
(1)①若PB=PC,連結PB,則∠PCB=∠PBC.
∵CD為等邊三角形的高.∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,∴PD=![]() DB=
DB=![]() AB.
AB.
與已知PD=![]() AB矛盾,∴PB≠PC.
AB矛盾,∴PB≠PC.
②若PA=PC,連結PA,
則∠PCA=∠PAC.
∵CD為等邊三角形的高.∴AD=BD,∠PCA=30°,
∴∠PAD=∠PAC=30°,∴PD=![]() DA=
DA=![]() AB.
AB.
與已知PD=![]() AB矛盾,∴PA≠PC.
AB矛盾,∴PA≠PC.
③若PA=PB,由PD=![]() AB,得PD=BD,
AB,得PD=BD,
∴∠BPD=45°,
故∠APB=90°;
(2)①若PB=PA,設PA=x,
∵∠C=90°,AB=13,BC=5,
∴AC=12,則CP=12-x,
∴x2=(12-x)2+52,
∴解得:x=![]() ,即PA=
,即PA=![]() .
.
②若PA=PC,則PA=6.
③若PC=PB,由圖知,
在Rt△PBC中,不可能,
故PA=![]() 或6.
或6.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,垂足為
,垂足為![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點.現(xiàn)有下列四個結論:①
的中點.現(xiàn)有下列四個結論:①![]() ;②四邊形
;②四邊形![]() 的面積等于
的面積等于![]() ;③
;③![]() ;④
;④![]() .其中正確結論的個數(shù)為( )
.其中正確結論的個數(shù)為( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,直線a、b、c表示三條公路,現(xiàn)要建一個貨物中轉站,要求它到三條公路的距離相等,則可供選擇的地址有_______處.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,![]() 和
和![]() 都是等邊三角形,點
都是等邊三角形,點![]() 、
、![]() 、
、![]() 在同一條直線上,
在同一條直線上,![]() 、
、![]() 分別與
分別與![]() 、
、![]() 交于點
交于點![]() 、
、![]() ,
,![]() 和
和![]() 交于點
交于點![]() ,有如下結論:①
,有如下結論:①![]() 是等邊三角形;②
是等邊三角形;②![]() ;③
;③![]() ≌
≌![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]() ;⑥
;⑥![]() ;⑦
;⑦![]() .其中不正確的結論的個數(shù)是( )
.其中不正確的結論的個數(shù)是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠B=30°,邊AB的垂直平分線DE交AB于點E,交BC于點D.CD=3,則BC的長為( )

A. 6 B. 9 C. 6![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知二次函數(shù)![]() 的圖象如圖所示,對稱軸為直線
的圖象如圖所示,對稱軸為直線![]() ,則下列結論正確的是( )
,則下列結論正確的是( )

A. ![]() B. 方程
B. 方程![]() 的兩個根是
的兩個根是![]() ,
,![]()
C. ![]() D. 當
D. 當![]() 時,
時,![]() 隨
隨![]() 的增大而增大
的增大而增大
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
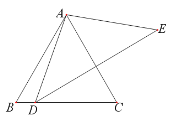
【題目】如圖,△ABC是等邊三角形,點D在BC上,△ADE是等腰三角形,AD =AE ,∠DAE =100°,當DE⊥AC時,求∠BAD和∠EDC的度數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
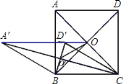
【題目】如圖,邊長為![]() 的正方形
的正方形![]() 的對角線交于點
的對角線交于點![]() ,把邊
,把邊![]() 、
、![]() 分別繞點
分別繞點![]() 、
、![]() 同時逆時針旋轉
同時逆時針旋轉![]() 得四邊形
得四邊形![]() ,其對角線交點為
,其對角線交點為![]() ,連接
,連接![]() .下列結論:
.下列結論:
①四邊形![]() 為菱形;
為菱形;
②![]() ;
;
③線段![]() 的長為
的長為![]() ;
;
④點![]() 運動到點
運動到點![]() 的路徑是線段
的路徑是線段![]() .其中正確的結論共有( )
.其中正確的結論共有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com