Question

【題目】 問題與探索

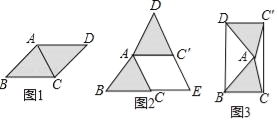
問題情境：課堂上，老師讓同學們以“菱形紙片的剪拼”為主題開展數學活動．如圖（1），將一張菱形紙片ABCD（∠BAD＞90°）沿對角線AC剪開，得到△ABC和△ACD．

操作發現：

（1）將圖（1）中的△ACD以點A為旋轉中心，按逆時針方向旋轉角α，使α=∠BAC，得到如圖（2）所示的△AC′D，分別延長BC和DC′交于點E，則四邊形ACEC′的形狀是 ．

（2）創新小組將圖（1）中的△ACD以點A為旋轉中心，按逆時針方向旋轉角α，使α=2∠BAC，得到如圖（3）所示的△AC′D，連接DB、C′C，得到四邊形BCC′D，發現它是矩形，請證明這個結論．

Answer 1

【答案】(1)菱形；(2)證明過程見解析

【解析】

試題分析：(1)、結論：菱形．首先證明四邊形ACEC′是平行四邊形，再由AC=AC′即可證明結論．

(2)、如圖3中，過點A作AE⊥C′C于點E，首先證明DC′∥CB，DC′=BC，推出四邊形BCC′D是平行四邊形，再證明∠BCC′=900即可．

試題解析：(1)、結論：菱形．理由：如圖2中，

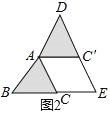
由題意∵AB=BC， ∴∠BAC=∠BCA=∠CAC′=∠AC′D ∴AC′∥EC， ∵∠CAC′=∠AC′D，

∴AC∥EC′， ∴四邊形ACEC′是平行四邊形， ∵AC=AC′， ∴四邊形ACEC′是菱形．

(2)、如圖3中，過點A作AE⊥C′C于點E，

由旋轉的性質，得AC′=AC， ∴∠CAE=∠C′AE=α=∠ABC，∠AEC=90°， ∵BA=BC，

∴∠BCA=∠BAC ∴∠CAE=∠BCA， ∴AE∥BC． 同理，AE∥DC′， ∴BC∥DC′，

又∵BC=DC′， ∴四邊形BCC′D是平行四邊形， 又∵AE∥BC，∠AEC=90°，

∴∠BCC′=1800﹣900=900 ∴四邊形BCC′D是矩形．