
【題目】安慶市在精準扶貧活動中,因地制宜指導農民調整種植結構,增加種植效益,2018年李大伯家在工作隊的幫助下,計劃種植馬鈴薯和蔬菜共15畝,預計每畝的投入與產出如下表:(每畝產出-每畝投入=每畝純收入)
種類 | 投入(元) | 產出(元) |
馬鈴薯 | 1000 | 4500 |
蔬菜 | 1200 | 5300 |
(1)如果這15畝地的純收入要達到54900元,需種植馬鈴薯和蔬菜各多少畝?
(2)如果總投入不超過16000元,則最多種植蔬菜多少畝?該情況下15畝地的純收入是多少?
【答案】(1)需種植馬鈴薯11畝,需種植蔬菜4畝;(2)最多種植蔬菜5畝,該情況下15畝地的純收入是55500元.
【解析】
(1)設需種植馬鈴薯x畝,需種植蔬菜y畝,根據等量關系:一共15畝地;這15畝地的純收入要達到54900元;列出關于x和y的二元一次方程組,解出即可;
(2)設種植馬鈴薯a畝,則需種植蔬菜(15-a)畝,根據“總投入不超過16000元”,列出關于a的一元一次不等式,解出即可.
(1)設需種植馬鈴薯![]() 畝,需種植蔬菜
畝,需種植蔬菜![]() 畝,依題意有
畝,依題意有
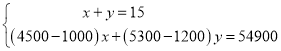 ,
,
解得![]() .
.
故需種植馬鈴薯11畝,需種植蔬菜4畝;
(2)設種植馬鈴薯![]() 畝,則需種植蔬菜
畝,則需種植蔬菜![]() 畝,依題意有
畝,依題意有
![]() ,
,
解得![]() ,
,
![]() (畝),
(畝),
![]()
![]()
![]() (元).
(元).
答:最多種植蔬菜5畝,該情況下15畝地的純收入是55500元.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:初中數學 來源: 題型:
【題目】定義:在平面直角坐標系中,點A、B為函數L圖象上的任意兩點,點A坐標為(x1 , y1),點B坐標為(x2 , y2),把式子 ![]() 稱為函數L從x1到x2的平均變化率;對于函數K:y=2x2﹣3x+1圖象上有兩點A(x1 , y1)和B(x2 , y2),當x1=1,x2﹣x1=
稱為函數L從x1到x2的平均變化率;對于函數K:y=2x2﹣3x+1圖象上有兩點A(x1 , y1)和B(x2 , y2),當x1=1,x2﹣x1= ![]() 時,函數K從x1到x2的平均變化率是;當x1=1,x2﹣x1=
時,函數K從x1到x2的平均變化率是;當x1=1,x2﹣x1= ![]() (n為正整數)時,函數K從x1到x2的平均變化率是 .
(n為正整數)時,函數K從x1到x2的平均變化率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學改革學生的學習模式,變“老師要學生學習”為“學生自主學習”,培養了學生自主學習的能力.李萌與和謝娜同學就“你最喜歡哪種學習方式”隨機調查了他們周圍的一些同學,根據收集到的數據繪制了以下兩個不完整的統計圖(如圖).

請根據上面兩個不完整的統計圖回答以下4個問題:
(1)這次抽樣調查中,共調查了 名學生.
(2)補全條形統計圖中的缺項.
(3)在扇形統計圖中,選擇教師傳授的所占圓心角的度數為 .
(4)根據調查結果,估算該校1800名學生中大約有多少人選擇小組合作學習模式?
查看答案和解析>>
科目:初中數學 來源: 題型:
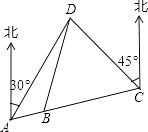
【題目】某市開展一項自行車旅游活動,線路需經A,B,C,D四地,如圖,其中A,B,C三地在同一直線上,D地在A地北偏東30°方向,在C地北偏西45°方向,C地在A地北偏東75°方向.且BC=CD=20km,問沿上述線路從A地到D地的路程大約是多少?(最后結果保留整數,參考數據:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,∠C=50°,AH,BD分別是△ABC高和角平分線,點P為邊BC上一個點,當△BDP為直角三角形時,則∠CDP=_____度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠A=90°,AB=AC,D為BC的中點.
(1)如圖1,寫出點D到△ABC三個頂點A,B,C的距離的關系(直接寫出結論);
(2)如圖1,點E,F分別是AB,AC上的點,且BE=AF,求證:△DEF是等腰直角三角形;
(3)若點E,F分別是AB,CA的延長線上的點,仍有BE=AF,其他條件不變,請判斷△DEF的形狀?(直接寫結論).


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】等腰三角形有如下性質:“在等腰三角形中,等邊對等角”.即:如圖1,在△ABC中,若AB=AC,則∠B=∠C.利用此性質解決以下問題:
如圖2,在四邊形ABCD中,AD∥BC,點E在邊AD上,且CB=CE,點F是射線ED上的一個動點,∠ECF的平分線CG交BE的延長線于點G.
(1)若∠EBC=68°,∠ECF=40°,求G的度數;
(2)在動點F運動的過程中,∠G:∠EFC的值是否發生變化?若不變,求它的值;若變化,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若x+y+z=15,-3x-y+z=-25,x、y、z皆為非負數,記整式5x+4y+z的最大值為a,最小值為b,則a﹣b =________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com