
【題目】如圖,在平面直角坐標系中,點![]() 的坐標是
的坐標是![]() ,動點
,動點![]() 從原點O出發,沿著
從原點O出發,沿著![]() 軸正方向移動,以
軸正方向移動,以![]() 為斜邊在第一象限內作等腰直角三角形
為斜邊在第一象限內作等腰直角三角形![]() ,設動點
,設動點![]() 的坐標為
的坐標為![]() .
.

(1)當![]() 時,點
時,點![]() 的坐標是 ;當
的坐標是 ;當![]() 時,點
時,點![]() 的坐標是 ;
的坐標是 ;
(2)求出點![]() 的坐標(用含
的坐標(用含![]() 的代數式表示);
的代數式表示);
(3)已知點![]() 的坐標為
的坐標為![]() ,連接
,連接![]() 、
、![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,求當
,求當![]() 為何值時,當
為何值時,當![]() 與
與![]() 全等.
全等.
【答案】(1) (2,2);(![]() ,
,![]() ); (2) P(
); (2) P(![]() ,
,![]() );(3)
);(3) ![]() .
.
【解析】
(1) 當![]() 時,三角形AOB為等腰直角三角形, 所以四邊形OAPB為正方形,直接寫出結果;當
時,三角形AOB為等腰直角三角形, 所以四邊形OAPB為正方形,直接寫出結果;當![]() 時,作PN⊥y軸于N,作PM⊥x軸與M,求出△BNP≌△AMP,即可得到ON+OM=OB-BN+OA+AM=OB+OA,即可求出;
時,作PN⊥y軸于N,作PM⊥x軸與M,求出△BNP≌△AMP,即可得到ON+OM=OB-BN+OA+AM=OB+OA,即可求出;
(2) 作PE⊥y軸于E,PF⊥x軸于F,求出△BEP≌△AFP,即可得到OE+OF=OB+BE+OA+AF=OB+OA,即可求出;
(3) 根據已知求出BC值,根據上問得到OQ=![]() ,△PQB≌△PCB,BQ=BC,因為OQ=BQ+OB,即可求出t.
,△PQB≌△PCB,BQ=BC,因為OQ=BQ+OB,即可求出t.
(1) 當![]() 時,三角形AOB為等腰直角三角形如圖
時,三角形AOB為等腰直角三角形如圖

所以四邊形OAPB為正方形,所以P(2,2)
當![]() 時,如圖
時,如圖
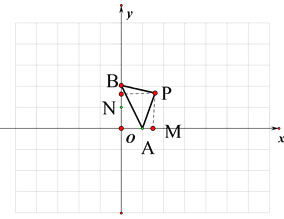
作PN⊥y軸于N,作PM⊥x軸與M
∴四邊形OMPN為矩形
∵∠BPN+∠NPA=∠APM+∠NPA=90°
∴ ∠BPN =∠APM
∵∠BNP=∠AMP
∴ △BNP≌△AMP
∴PN=PM BN=AM
∴四邊形OMPN為正方形,OM=ON=PN=PM
∴ON+OM=OB-BN+OA+AM=OB+OA=2+1=3
∴OM=ON=PN=PM=![]()
∴ P(![]() ,
,![]() )
)
(2) 如圖
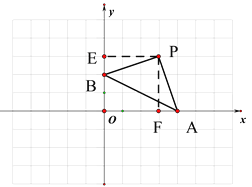
作PE⊥y軸于E,PF⊥x軸于F,則四邊形OEPF為矩形
∵∠BPE+∠BPF=∠APF+∠BPF=90°
∴ ∠BPE =∠APF
∵∠BEP=∠AFP
∴ △BEP≌△AFP
∴PE=PF BE=AF
∴四邊形OEPF為正方形,OE=OF=PE=PF
∴OE+OF=OB+BE+OA+AF=OB+OA=2+t
∴ OE=OF=PE=PF=![]()
∴ P(![]() ,
,![]() );
);
(3) 根據題意作PQ⊥y軸于Q,作PG⊥x軸與G
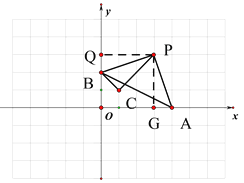
∵ B(0,2) C(1,1)
∴ BC=![]()
由上問可知P(![]() ,
,![]() ),OQ=
),OQ=![]()
∵△PQB≌△PCB
∴BC=QB=![]()
∴ OQ=BQ+OB=![]() +2=
+2=![]()
解得 t=![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在邊長為2的正方形ABCD中剪去一個邊長為1的小正方形CEFG,動點P從點A出發,沿A→D→E→F→G→B的路線繞多邊形的邊勻速運動到點B時停止(不含點A和點B),則△ABP的面積S隨著時間t變化的函數圖象大致是( )

A.  B.
B. 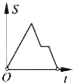 C.
C. 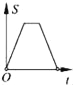 D.
D. 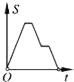
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們定義:如果一個等腰三角形有一條邊長是3,那么這個三角形稱作帥氣等腰三角形.已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,在
,在![]() 所在平面內畫一條直線,將
所在平面內畫一條直線,將![]() 分割成兩個三角形,若其中一個三角形是帥氣等腰三角形,則這樣的直線最多可畫( )
分割成兩個三角形,若其中一個三角形是帥氣等腰三角形,則這樣的直線最多可畫( )
A.0條B.1條C.2條D.3條
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的周長為17,點D,E在邊BC上,∠ABC的平分線垂直于AE,垂足為點N,∠ACB的平分線垂直于AD,垂足為點M,若BC=6,則MN的長度為_____.
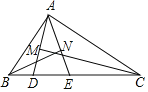
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把一個等腰直角三角形![]() 沿斜邊上的高
沿斜邊上的高![]() 剪下,與剩下部分能拼成一個平行四邊形
剪下,與剩下部分能拼成一個平行四邊形![]() ,如圖(1).
,如圖(1).
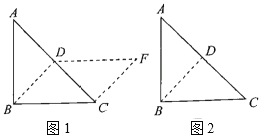
(1)想一想,判斷四邊形![]() 是平行四邊形的依據是_____________________________________.(用平行四邊形的判定方法敘述)
是平行四邊形的依據是_____________________________________.(用平行四邊形的判定方法敘述)
(2)按上述方法做一做,請你拼一個與圖(1)位置或形狀不同的平行四邊形。并在圖(2)中面出示意圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx(a≠0) 交x軸正半軸于點A,直線y=2x 經過拋物線的頂點M.已知該拋物線的對稱軸為直線x=2,交x軸于點B.

(1)求a,b的值;
(2)P是第一象限內拋物線上的一點,且在對稱軸的右側,連接OP,BP.設點P的橫坐標為m ,△OBP的面積為S,![]() .求K關于m 的函數表達式及K的范圍.
.求K關于m 的函數表達式及K的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的情景對話,然后解答問題:
老師:我們定義一種三角形,兩邊的平方和等于第三邊平方的2倍的三角形叫做奇異三角形.
小華:等邊三角形一定是奇異三角形!
小明:那直角三角形中是否存在奇異三角形呢?

問題(1):根據“奇異三角形”的定義,請你判斷小華提出的猜想:“等邊三角形一定是奇異三角形”是否正確?___________填“是”或“否”)
問題(2):已知![]() 中,兩邊長分別是5,
中,兩邊長分別是5,![]() ,若這個三角形是奇異三角形,則第三邊長是_____________;
,若這個三角形是奇異三角形,則第三邊長是_____________;
問題(3):如圖,以![]() 為斜邊分別在
為斜邊分別在![]() 的兩側作直角三角形,且
的兩側作直角三角形,且![]() ,若四邊形
,若四邊形![]() 內存在點
內存在點![]() ,使得
,使得![]() ,
,![]() .試說明:
.試說明:![]() 是奇異三角形.
是奇異三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,下列條件不能判定四邊形ABCD是矩形的是( )

A.∠DAB=∠ABC=∠BCD=90°B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DOD.AO=BO=CO=DO
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個木箱中裝有卡片共50張,這些卡片共有三種,它們分別標有1、2、3的字樣,除此之外其他都相同,其中標有數字2卡片的張數是標有數字3卡片的張數的3倍少8張.已知從箱子中隨機摸出一張標有數字1卡片的概率是![]() .
.
(1)求木箱中裝有標1的卡片張數;
(2)求從箱子中隨機摸出一張標有數字3的卡片的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com