
【題目】在△ABC中,∠B=40°,AD是BC邊上的高,且∠DAC=20°,則∠BAC=________.
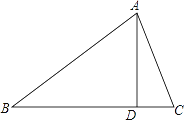
【答案】70°
【解析】∵∠B=40°,AD⊥BC,
∴∠BAD=90°-40°=50°.
∵∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°.
【題型】填空題
【結束】
16
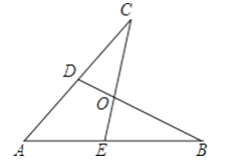
【題目】如圖所示,E,D是AB,AC上的兩點,BD,CE交于點O,且AB=AC,使△ACE≌△ABD,你補充的條件是________
 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案科目:初中數學 來源: 題型:
【題目】某中學數學活動小組為了調查居民的用水情況,從某社區的1500戶家庭中隨機抽取了30戶家庭的月用水量,結果如下表所示:
月用水量(噸) | 3 | 4 | 5 | 7 | 8 | 9 | 10 |
戶 數 | 4 | 3 | 5 | 11 | 4 | 2 | 1 |
(1)求這30戶家庭月用水量的平均數,眾數和中位數;
(2)根據上述數據,試估計該社區的月用水量;
(3)由于我國水資源缺乏,許多城市常利用分段計費的辦法引導人們節約用水,即規定每個家庭的月基本用水量為m(噸),家庭月用水量不超過m(噸)的部分按原價收費,超過m噸部分加倍收費,你認為上述問題中的平均數、眾數、中位數中哪一個量作為月基本用水量比較合理?簡述理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某次籃球聯賽初賽階段,每隊有![]() 場比賽,每場比賽都要分出勝負,每隊勝一場得
場比賽,每場比賽都要分出勝負,每隊勝一場得![]() 分, 負一場得
分, 負一場得![]() 分,積分超過
分,積分超過![]() 分才能獲得參賽資格.
分才能獲得參賽資格.
(1)已知甲隊在初賽階段的積分為![]() 分,求甲隊初賽階段勝、負各多少場;
分,求甲隊初賽階段勝、負各多少場;
(2)如果乙隊要獲得參加決賽資格,那么乙隊在初賽階段至少要勝多少場?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校準備租用一批汽車,現有甲、乙兩種大客車,甲種客車每輛載客量45人,乙種客車每輛載客量30人,已知1輛甲種客車和3輛乙種客車共需租金1240元,3輛甲種客車和2輛乙種客車共需租金1760元.
(1)求1輛甲種客車和1輛乙種客車的租金分別是多少元?
(2)學校計劃租用甲、乙兩種客車共8輛,送330名師生集體外出活動,最節省的租車費用是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠BAC的平分線交BC于點D,DE⊥AD,交AB于點E,AE為⊙O的直徑 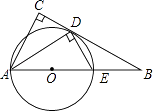
(1)判斷BC與⊙O的位置關系,并證明你的結論;
(2)求證:△ABD∽△DBE;
(3)若cosB= ![]() ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(題文)(問題引領)
問題1:在四邊形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分別是AB,AD上的點.且∠ECF=60°.探究圖中線段BE,EF,FD之間的數量關系.
小王同學探究此問題的方法是,延長FD到點G.使DG=BE.連結CG,先證明
△CBE≌△CDG,再證明△CEF≌△CGF.他得出的正確結論是________________.

(探究思考)
問題2:若將問題1的條件改為:四邊形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF= ![]() ∠BCD, 問題1的結論是否仍然成立?請說明理由.
∠BCD, 問題1的結論是否仍然成立?請說明理由.

(拓展延伸)
問題3:在問題2的條件下,若點E在AB的延長線上,點F在DA的延長線上,則問題2的結論是否仍然成立?若不成立,猜測此時線段BE、DF、EF之間存在什么樣的等量關系?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,已知直線y=x上一點P(1,1),C為y軸上一點,連接PC,線段PC繞點P順時針旋轉90°至線段PD,過點D作直線AB⊥x軸,垂足為B;直線AB與直線y=x交于點A,連接CD,直線CD與直線y=x交于點Q.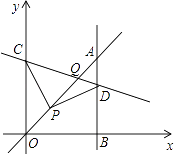
(1)求證:OB=OC;
(2)當點C坐標為(0,3)時,求點Q的坐標;
(3)當△OPC≌△ADP時,直接寫出C點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com