
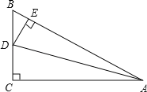
【題目】如圖△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,給出下列結論:①DC=DE;②DA平分∠CDE;③DE平分∠ADB;④BE+AC=AB;⑤∠BAC=∠BDE.其中正確的是_____ (寫序號)
【答案】①②④⑤
【解析】
根據角平分線上的點到角的兩邊的距離相等可得DC=DE,判斷①正確,然后利用“HL”證明Rt△ACD和Rt△AED全等,根據全等三角形對應角相等可得∠ADC=∠ADE,判斷②正確;全等三角形對應邊相等可得AC=AE,然后求出BE+AC=AB,判斷④正確;根據同角的余角相等求出∠BAC=∠BDE,判斷⑤正確,并得到③錯誤.
解:∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴DC=DE,故①正確;
在Rt△ACD和Rt△AED中,![]() ,
,
∴Rt△ACD≌Rt△AED(HL),
∴∠ADC=∠ADE,AC=AE,
∴DA平分∠CDE,故②正確;
BE+AC=BE+AE=AB,故④正確;
∵∠BAC+∠B=90°,
∠BDE+∠B=90°,
∴∠BAC=∠BDE,故⑤正確;
∵∠ADE+∠BAD=90°,而∠BAD≠∠B,
∴∠BDE≠∠ADE,
∴DE平分∠ADB錯誤,故③錯誤;
綜上所述,正確的有①②④⑤.
故答案為:①②④⑤.


科目:初中數學 來源: 題型:
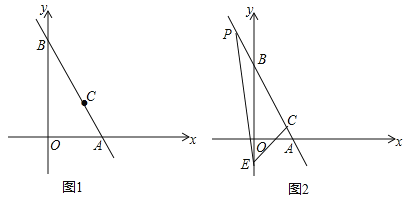
【題目】如圖1,在平面直角坐標系中,直線AB經過點C(a,a),且交x軸于點A(m,0),交y軸于點B(0,n),且m,n滿足![]() +(n﹣12)2=0.
+(n﹣12)2=0.
(1)求直線AB的解析式及C點坐標;
(2)過點C作CD⊥AB交x軸于點D,請在圖1中畫出圖形,并求D點的坐標;
(3)如圖2,點E(0,﹣2),點P為射線AB上一點,且∠CEP=45°,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
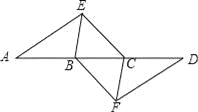
【題目】如圖,點A,B,C,D在同一條直線上,點E,F分別在直線AD的兩側,且AE=DF,∠A=∠D,AB=DC.
(1)求證:四邊形BFCE是平行四邊形;
(2)若AD=10,DC=3,∠EBD=60°,則BE= 時,四邊形BFCE是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
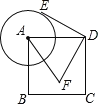
【題目】如圖,已知正方形 ABCD 的邊長為 2,以點 A 為圓心,1 為半徑作圓,點 E 是⊙A 上的任意 一點,點 E 繞點 D 按逆時針方向轉轉 90°,得到點 F,接 AF,則 AF 的最大值是______________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場購進一批 30 瓦的 LED 燈泡和普通白熾燈泡進行銷售,其進價與標價如下表:
LED 燈泡 | 普通白熾燈泡 | |
進價(元) | 45 | 25 |
標價(元) | 60 | 30 |

(1)該商場購進了 LED 燈泡與普通白熾燈泡共 300 個,LED 燈泡按標價進行銷售,而普通 白熾燈泡打九折銷售,當銷售完這批燈泡后可獲利 3 200 元,求該商場購進 LED 燈泡與 普通白熾燈泡的數量分別為多少個?
(2)由于春節期間熱銷,很快將兩種燈泡銷售完,若該商場計劃再次購進這兩種燈泡 120 個, 在不打折的情況下,請問如何進貨,銷售完這批燈泡時獲利最多且不超過進貨價的 30%, 并求出此時這批燈泡的總利潤為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某人駕車從![]() 地出發在一條筆直的南北方向上來回行駛,向北行駛為正,向南行駛為負,行駛的路程情況如下(單位:千米):
地出發在一條筆直的南北方向上來回行駛,向北行駛為正,向南行駛為負,行駛的路程情況如下(單位:千米):![]() .
.
![]() 該人在完成上述
該人在完成上述![]() 次行車后在
次行車后在![]() 地的哪一側?距
地的哪一側?距![]() 地多少千米?
地多少千米?
![]() 如果這輛車每行駛
如果這輛車每行駛![]() 千米的耗油量為
千米的耗油量為![]() 升,這一天共耗油多少升?
升,這一天共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是【 】
A.若甲組數據的方差![]() ,乙組數據的方差
,乙組數據的方差![]() ,則甲組數據比乙組數據大
,則甲組數據比乙組數據大
B.從1,2,3,4,5,中隨機抽取一個數,是偶數的可能性比較大
C.數據3,5,4,1,﹣2的中位數是3
D.若某種游戲活動的中獎率是30%,則參加這種活動10次必有3次中獎
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,在△ABC中,∠ACB=90°,AC=BC,直線l過點C,點A,B在直線l同側,BD⊥l,AE⊥l,垂足分別為D,E.求證:△AEC≌△CDB.
(2)如圖2,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,利用(1)中的結論,請按照圖中所標注的數據計算圖中實線所圍成的圖形的面積S= .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com