
【題目】已知△ABC的外角∠CBE,∠BCF的角平分線BP,CP交于P點,則∠BPC是( )
A.鈍角
B.銳角
C.直角
D.無法確定
【答案】B
【解析】解: 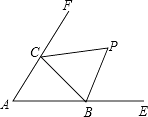
∵△ABC的外角平分線BP,CP交于P點,
∴∠PBC= ![]() ∠EBC,∠BCP=
∠EBC,∠BCP= ![]() ∠BCF,
∠BCF,
∵∠CBE、∠BCF是△ABC的兩個外角,
∴∠CBE+∠BCF=360°﹣(180°﹣∠A)=180°+∠A,
∴∠PBC+∠BCP= ![]() (∠EBC+∠BCF)=
(∠EBC+∠BCF)= ![]() (180°+∠A)=90°+
(180°+∠A)=90°+ ![]() ∠A,
∠A,
∵在△PBC中,∠BPC=180°﹣(∠PBC+∠BCP)=180°﹣(90°+ ![]() ∠A)=90°﹣
∠A)=90°﹣ ![]() ∠A<90°,
∠A<90°,
∴∠BPC是銳角.
故選:B.
首先根據△ABC的外角平分線BP,CP交于P點,得出∠PBC+∠BCP=90°+ ![]() ∠A,再根據三角形內角和定理,求得∠BPC=90°﹣
∠A,再根據三角形內角和定理,求得∠BPC=90°﹣ ![]() ∠A<90°即可.
∠A<90°即可.


科目:初中數學 來源: 題型:
【題目】已知直線l1∥l2 , 且l4和l1、l2分別交于A、B兩點,點P為線段AB上的一個定點如圖1) 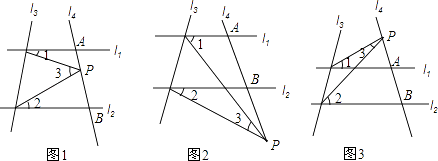
(1)寫出∠1、∠2、∠3、之間的關系并說出理由.
(2)如果點P為線段AB上的動點時,問∠1、∠2、∠3之間的關系是否發生變化?(必說理由)
(3)如果點P在A、B兩點外側運動時,(點P和點A、點B不重合)
①如圖2,當點P在射線AB上運動時,∠1、∠2、∠3之間關系并說出理由.
②如圖3,當點P在射線BA上運動時,∠1、∠2、∠3之間關系(不說理由)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,EF∥AD,∠1=∠2.說明:∠DGA+∠BAC=180°.請將說明過程填寫完成.
解:∵EF∥AD,(已知)
∴∠2= . ()
又∵∠1=∠2,()
∴∠1=∠3,()
∴AB∥ , ()
∴∠DGA+∠BAC=180°.()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com