
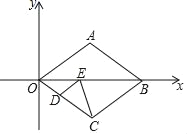
【題目】如圖,在平面直角坐標(biāo)系中,菱形OABC的頂點(diǎn)A的坐標(biāo)為(4,3),點(diǎn)D是邊OC上的一點(diǎn),點(diǎn)E在直線OB上,連接DE、CE,則DE+CE的最小值為( )
A. 5B. ![]() +1C. 2
+1C. 2![]() D.
D. ![]()
【答案】D
【解析】
首先根據(jù)菱形的對(duì)角線性質(zhì)得到DE+CE的最小值=CF,再利用菱形的面積列出等量關(guān)系即可解題.
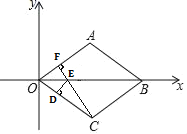
解:如下圖,過(guò)點(diǎn)C作CF⊥OA與F,交OB于點(diǎn)E,過(guò)點(diǎn)E作ED⊥OC與D,
∵四邊形OABC是菱形,由菱形對(duì)角線互相垂直平分可知EF=ED,
∴DE+CE的最小值=CF,
∵A的坐標(biāo)為(4,3),
∴對(duì)角線分別是8和6,OA=5,
∴菱形的面積=24,(二分之一對(duì)角線的乘積),
即24=CF×5,
解得:CF= ![]() ,
,
即DE+CE的最小值=![]() ,
,
故選D.


 靈星計(jì)算小達(dá)人系列答案
靈星計(jì)算小達(dá)人系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在Rt△ABC中,已知∠C=90°,∠A=60°,AC=3cm,以斜邊AB的中點(diǎn)P為旋轉(zhuǎn)中心,把這個(gè)三角形按逆時(shí)針?lè)较蛐D(zhuǎn)90°得到Rt△A′B′C′,則旋轉(zhuǎn)前后兩個(gè)直角三角形重疊部分的面積為______________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
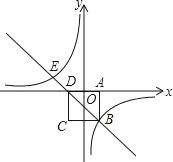
【題目】如圖,在平面直角坐標(biāo)系中,邊長(zhǎng)為2的正方形ABCD關(guān)于y軸對(duì)稱(chēng),邊AD在x軸上,點(diǎn)B在第四象限,直線BD與反比例函數(shù)![]() 的圖象交于點(diǎn)B、E.
的圖象交于點(diǎn)B、E.
(1)求反比例函數(shù)及直線BD的解析式;
(2)求點(diǎn)E的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】把下面的有理數(shù)填在相應(yīng)的大括號(hào)里:(★友情提示:將各數(shù)用逗號(hào)分開(kāi))
15,-![]() , 0,-0.15, -128,
, 0,-0.15, -128, ![]() ,+20,-2.6
,+20,-2.6
正數(shù)集合 { . . . ﹜;
負(fù)數(shù)集合 ﹛ . . . ﹜;
整數(shù)集合 ﹛ . . . ﹜;
非負(fù)數(shù)集合 ﹛ . . . ﹜.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
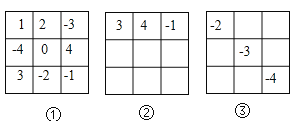
【題目】如圖的圖例①是一個(gè)方陣圖,每行的3個(gè)數(shù)、每列的3個(gè)數(shù)、斜對(duì)角的3個(gè)數(shù)相加的和均相等.如果將方陣圖的每個(gè)數(shù)都加上同一個(gè)數(shù),那么方陣中每行的3個(gè)數(shù)、每列的3個(gè)數(shù)、斜對(duì)角的3個(gè)數(shù)相加的和仍然相等,這樣就形成新的方陣圖.
根據(jù)圖①②③中給出的數(shù),對(duì)照原來(lái)的方陣圖,請(qǐng)你完成圖②③的方陣圖?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某檢修小組1乘一輛汽車(chē)沿公路檢修線路,約定向東為正。某天從A地出發(fā)到收工時(shí),行走記錄為(單位:千米):+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6。另一小組2也從A地出發(fā),在南北向修,約定向北為正,行走記錄為:-17,+9,-2,+8,+6,+9,-5,-1,+4,-7,-8.
(1)分別計(jì)算收工時(shí),1,2兩組在A地的哪一邊,距A地多遠(yuǎn)?
(2)若每千米汽車(chē)耗油a升,求出發(fā)到收工各耗油多少升?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
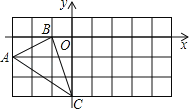
【題目】如圖,在平面直角坐標(biāo)系中,△ABC的三個(gè)頂點(diǎn)坐標(biāo)分別為A(﹣3,﹣1)、B(﹣1,0)、C(0,﹣3)
(1)點(diǎn)A關(guān)于坐標(biāo)原點(diǎn)O對(duì)稱(chēng)的點(diǎn)的坐標(biāo)為 .
(2)將△ABC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)90°,畫(huà)出旋轉(zhuǎn)后得到的△A1B1C,A1A的長(zhǎng)為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】周末,小華騎自行車(chē)從家出發(fā)到植物園玩,從家出發(fā) 1 小時(shí)后,因自行車(chē)損壞修理了一段時(shí)間后,按原速前往植物園,小華從家出發(fā) 1 小時(shí) 50 分后,爸爸從家出發(fā)騎摩托車(chē)沿相同路線前往植物園,如圖是他們家的路程 y(km)與小華離家的時(shí)間 x(h)的函數(shù)圖象,已知爸爸騎摩托車(chē)的速度是小華騎車(chē)速度的 2 倍,若爸爸比小華早 10 分達(dá)到植物園,則小華家到植物園的路程是_____km.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
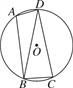
【題目】如圖,已知四邊形ABCD內(nèi)接于圓O,連接BD,∠BAD=105°,∠DBC=75°.
(1)求證:BD=CD;
(2)若圓O的半徑為3,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com