
(11·湖州)(本小題10分)
我市水產養殖專業戶王大爺承包了30畝水塘,分別養殖甲魚和桂魚,有關成本、銷售情況如下表:
⑴2010年,王大爺養殖甲魚20畝,桂魚10畝,求王大爺這一年共收益多少萬元?(收益=銷售額-成本)
⑵2011年,王大爺繼續用這30畝水塘全部養殖甲魚和桂魚,計劃投入成本不超過70萬元。若每畝養殖的成本、銷售額與2010年相同,要獲得最大收益,他應養殖甲魚和桂魚各多少畝?
⑶已知甲魚每畝需要飼料500㎏,桂魚每畝需要飼料700㎏,根據⑵中的養殖畝數,為了節約運輸成本,實際使用的運輸車輛每次裝載飼料的總量是原計劃每次裝載總量的2倍,結果運輸養殖所需要全部飼料比原計劃減少了2次,求王大爺原定的運輸車輛每次可裝載飼料多少㎏?
解:⑴2010年王大爺的收益為:
20×(3-2.4)+10×(2.5-2)……………………………………………………2分
=17(萬元)…………………………………………………………………………2分
⑵設養殖甲魚x畝,則養殖桂魚(30-x)畝
則題意得2.4x+2(30-x)≤70
解得x≤25,……………………………………………………………………………………2分
又設王大爺可獲得收益為y萬元,
則y=0.6x+0.5(30-x),
即y=![]() .…………………………………………………………………………………1分
.…………………………………………………………………………………1分
∵函數值y隨x的增大而增大,
∴當x=25時,可獲得最大收益。
答:要獲得最大收益,應養殖甲魚25畝,桂魚5畝。……………………………………1分
⑶設大爺原定的運輸車輛每次可裝載飼料a㎏
由⑵得,共需要飼料為500×25+700×5=16000㎏,
根據題意得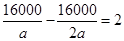 ,……………………………………………………1分
,……………………………………………………1分
解得a=4000㎏。………………………………………………………………………1分
答:王大爺原定的運輸車輛每次可裝載飼料4000㎏。
解析:略


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案科目:初中數學 來源: 題型:
(11·湖州)(本小題10分)
如圖,已知E、F分別是□ABCD的邊BC、AD上的點,且BE=DF。
⑴求證:四邊形AECF是平行四邊形;
⑵若BC=10,∠BAC=90°,且四邊形AECF是菱形,求BE的長。
查看答案和解析>>
科目:初中數學 來源: 題型:
(11·湖州)(本小題8分)
班主任張老師為了了解學生課堂發言情況,對前一天本班男、女生發言次數進行了統計,并
繪制成如下頻數分布折線圖(圖1)。
⑴請根據圖1,回答下列問題:
①這個班共有 ▲ 名學生,發言次數是5次的男生有 ▲ 人、女生有 ▲ 人;
②男、女生發言次數的中位數分別是 ▲ 次和 ▲ 次;
⑵通過張老師的鼓勵,第二天的發言次數比前一天明顯增加,全班發言次數變化的人數的扇形統計圖如圖2所示,求第二天發言次數增加3次的學生人數和全班增加的發言總次數。
查看答案和解析>>
科目:初中數學 來源: 題型:
(11·湖州)(本小題8分)
如圖,已知AB是⊙O的直徑,弦CD⊥AB,垂足為E,∠AOC=60°,OC=2。
⑴求OE和CD的長;
⑵求圖中陰影部隊的面積。
查看答案和解析>>
科目:初中數學 來源: 題型:
(11·湖州)(本小題6分)
已知:一次函數y=kx+b的圖象經過M(0,2),(1,3)兩點。
⑴求k,b的值;
⑵若一次函數y=kx+b的圖象與x軸交點為A(a,0),求a的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com