
【題目】如圖,矩形OABC的頂點(diǎn)A、C分別在x、y的正半軸上,點(diǎn)B的坐標(biāo)為(3,4),一次函數(shù) ![]() 的圖象與邊OC、AB分別交于點(diǎn)D、E,并且滿足OD=BE.點(diǎn)M是線段DE上的一個動點(diǎn).
的圖象與邊OC、AB分別交于點(diǎn)D、E,并且滿足OD=BE.點(diǎn)M是線段DE上的一個動點(diǎn).
(1)求b的值;
(2)連結(jié)OM,若三角形ODM的面積與四邊形OAEM的面積之比為1:3,求點(diǎn)M的坐標(biāo);
(3)設(shè)點(diǎn)N是x軸上方平面內(nèi)的一點(diǎn),以O(shè)、D、M、N為頂點(diǎn)的四邊形是菱形,求點(diǎn)N的坐標(biāo).
【答案】
(1)
解: ![]() 中,令x=0,解得y=b,則D的坐標(biāo)是(0,b),OD=b,
中,令x=0,解得y=b,則D的坐標(biāo)是(0,b),OD=b,
∵OD=BE,
∴BE=b,則E的坐標(biāo)是(3,4﹣b),
把E的坐標(biāo)代入 ![]() 得4﹣b=﹣2+b,
得4﹣b=﹣2+b,
解得:b=3
(2)
解:S四邊形OAED= ![]() (OD+AE)OA=
(OD+AE)OA= ![]() ×(3+1)×3=6,
×(3+1)×3=6,
∵三角形ODM的面積與四邊形OAEM的面積之比為1:3,
∴S△ODM=1.5.
設(shè)M的橫坐標(biāo)是a,則 ![]() ×3a=1.5,
×3a=1.5,
解得:a=1,
把x=a=1代入y=﹣ ![]() x+3得y=﹣
x+3得y=﹣ ![]() ×
× ![]() +3=
+3= ![]() .
.
則M的坐標(biāo)是(1, ![]() )
)
(3)
解:當(dāng)四邊形OMDN是菱形時,如圖(1),

M的縱坐標(biāo)是 ![]() ,把y=
,把y= ![]() 代入y=﹣
代入y=﹣ ![]() x+3,得﹣
x+3,得﹣ ![]() x+3=
x+3= ![]() ,解得:x=
,解得:x= ![]() ,
,
則M的坐標(biāo)是( ![]() ,
, ![]() ),
),
則N的坐標(biāo)是(﹣ ![]() ,
, ![]() );
);
當(dāng)四邊形OMND是菱形時,如圖(2)
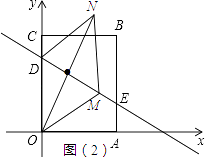
OM=OD=3,設(shè)M的橫坐標(biāo)是m,則縱坐標(biāo)是﹣ ![]() m+3,
m+3,
則m2+(﹣ ![]() m+3)2=9,
m+3)2=9,
解得:m= ![]() 或0(舍去).
或0(舍去).
則M的坐標(biāo)是( ![]() ,
, ![]() ).
).
則DM的中點(diǎn)是( ![]() ,
, ![]() ).
).
則N的坐標(biāo)是( ![]() ,
, ![]() ).
).
故N的坐標(biāo)是(﹣ ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
【解析】(1)首先在一次函數(shù)的解析式中令x=0,即可求得D的坐標(biāo),則OD的長度即可求得,OD=b,則E的坐標(biāo)即可利用b表示出來,然后代入一次函數(shù)解析式即可得到關(guān)于b的方程,求得b的值;(2)首先求得四邊形OAED的面積,則△ODM的面積即可求得,設(shè)出M的橫坐標(biāo),根據(jù)三角形的面積公式即可求得M的橫坐標(biāo),進(jìn)而求得M的坐標(biāo);(3)分成四邊形OMDN是菱形和四邊形OMND是菱形兩種情況進(jìn)行討論,四邊形OMDN是菱形時,M是OD的中垂線與DE的交點(diǎn),M關(guān)于OD的對稱點(diǎn)就是N;
四邊形OMND是菱形,OM=OD,M在直角DE上,設(shè)出M的坐標(biāo),根據(jù)OM=OD即可求得M的坐標(biāo),則根據(jù)ON和DM的中點(diǎn)重合,即可求得N的坐標(biāo).
【考點(diǎn)精析】根據(jù)題目的已知條件,利用菱形的性質(zhì)和矩形的性質(zhì)的相關(guān)知識可以得到問題的答案,需要掌握菱形的四條邊都相等;菱形的對角線互相垂直,并且每一條對角線平分一組對角;菱形被兩條對角線分成四個全等的直角三角形;菱形的面積等于兩條對角線長的積的一半;矩形的四個角都是直角,矩形的對角線相等.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
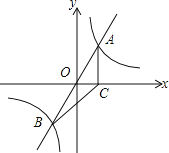
【題目】如圖,直線y=mx與雙曲線y=![]() 相交于A、B兩點(diǎn),A點(diǎn)的坐標(biāo)為(1,2),AC⊥x軸于C,連結(jié)BC.
相交于A、B兩點(diǎn),A點(diǎn)的坐標(biāo)為(1,2),AC⊥x軸于C,連結(jié)BC.
(1)求反比例函數(shù)的表達(dá)式;
(2)根據(jù)圖象直接寫出當(dāng)mx>![]() 時,x的取值范圍;
時,x的取值范圍;
(3)在平面內(nèi)是否存在一點(diǎn)D,使四邊形ABDC為平行四邊形?若存在,請求出點(diǎn)D坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為全面開展“陽光大課間”活動,某中學(xué)三個年級準(zhǔn)備成立“足球”、“籃球”、“跳繩”、“踢毽”四個課外活動小組,學(xué)校體育組根據(jù)七年級學(xué)生的報名情況(每人限報一項)繪制了兩幅不完整的統(tǒng)計圖(如圖),
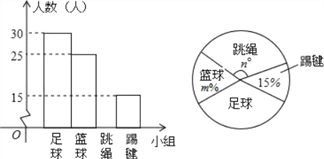
請根據(jù)以上信息,完成下列問題:
(1)m= ,n= ,并將條形統(tǒng)計圖補(bǔ)充完整;
(2)根據(jù)七年級的報名情況,試問全校2000人中,大約有多少人報名參加足球活動小組?
(3)根據(jù)活動需要,從“跳繩”小組的二男二女四名同學(xué)中隨機(jī)選取兩人到“踢毽”小組參加訓(xùn)練,請用列表或樹狀圖的方法計算恰好選中一男一女兩名同學(xué)的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下列因式分解的過程,再回答提出的問題:
1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(1+x)]=(1+x)(1+x)2=(1+x)3,若分解1+x+x(1+x)+x(1+x)2+…+x(1+x)2017結(jié)果是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,動點(diǎn)A從原點(diǎn)出發(fā)向數(shù)軸負(fù)方向運(yùn)動,同時動點(diǎn)B也從原點(diǎn)出發(fā)向數(shù)軸正方向運(yùn)動,2秒后,兩點(diǎn)相距16個單位長度.已知動點(diǎn)A、B的速度比為1∶3(速度單位:1個單位長度/秒).

(1)求兩個動點(diǎn)運(yùn)動的速度;
(2)在數(shù)軸上標(biāo)出A、B兩點(diǎn)從原點(diǎn)出發(fā)運(yùn)動2秒時的位置;
(3)若表示數(shù)0的點(diǎn)記為O,A、B兩點(diǎn)分別從(2)中標(biāo)出的位置同時向數(shù)軸負(fù)方向運(yùn)動,再經(jīng)過多長時間,滿足OB=2OA?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】計如下表:
最高氣溫(℃) | 25 | 26 | 27 | 28 |
天 數(shù) | 1 | 1 | 2 | 3 |
則這組數(shù)據(jù)的中位數(shù)與眾數(shù)分別是( )
A.27,28B.27.5,28C.28,27D.26.5,27
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某班去體育用品商店購買羽毛球和羽毛球拍,每只羽毛球2元,每副羽毛球拍25元.甲商店說:“羽毛球拍和羽毛球都打9折優(yōu)惠”,乙商店說:“買一副羽毛球拍贈2只羽毛球”.
(1)該班如果買2副羽毛球拍和20只羽毛球,問在甲、乙兩家商店各需花多少錢?
(2)該班如果準(zhǔn)備花90元錢全部用于買2副羽毛球拍和若干只羽毛球,請問到哪家商店購買更合算?
(3)該班如果必須買2副羽毛球拍,問當(dāng)買多少只羽毛球時到兩家商店購買同樣合算?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】李老師為了了解所教班級學(xué)生完成數(shù)學(xué)課前預(yù)習(xí)的具體情況,對本班部分學(xué)生進(jìn)行了為期半個月的跟蹤調(diào)查,他將調(diào)查結(jié)果分為四類:A、很好;B、較好;C、一般;D、較差,并將調(diào)查結(jié)果繪制成以下兩幅不完整的統(tǒng)計圖,請你根據(jù)統(tǒng)計圖解答下列問題:
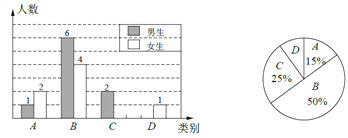
(1)李老師一共調(diào)查了多少名同學(xué)?
(2)C類女生有 名,D類男生有 名,將上面條形統(tǒng)計圖補(bǔ)充完整;
(3)為了共同進(jìn)步,李老師想從被調(diào)查的A類和D類學(xué)生中各隨機(jī)選取一位同學(xué)進(jìn)行“一幫一”互助學(xué)習(xí),請用列表法或畫樹形圖的方法求出所選兩位同學(xué)恰好是一位男同學(xué)和一位女同學(xué)的概率。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com