【題目】在如圖中，每個正方形由邊長為1的小正方形組成：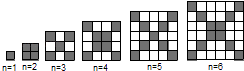
（1）觀察圖形，請填寫下列表格：
正方形邊長 | 1 | 3 | 5 | 7 | … | n（奇數） |
黑色小正方形個數 |
正方形邊長 | 2 | 4 | 6 | 8 | … | n（偶數） |
黑色小正方形個數 |
（2）在邊長為n（n≥1）的正方形中，設黑色小正方形的個數為P1 ， 白色小正方形的個數為P2 ， 問是否存在偶數n，使P2=5P1？若存在，請寫出n的值；若不存在，請說明理由．
【答案】
（1）1,5,9,13,2n﹣1,4,8,12,16,2n
（2）解：由（1）可知n為偶數時P1=2n，白色與黑色的總數為n2，
∴P2=n2﹣2n，
根據題意假設存在，則n2﹣2n=5×2n，
n2﹣12n=0，
解得n=12，n=0（不合題意舍去）．
存在偶數n=12使得P2=5P1．
【解析】解：（1）
正方形邊長 | 1 | 3 | 5 | 7 | … | n（奇數） |
黑色小正方形個數 | 1 | 5 | 9 | 13 | … | 2n﹣1 |
正方形邊長 | 2 | 4 | 6 | 8 | … | n（偶數） |
黑色小正方形個數 | 4 | 8 | 12 | 16 | … | 2n |
（1）根據題中圖形可以相應的完善表格，從而得出其規律.
（2）由（1）可知n為偶數時P1=2n，白色與黑色的總數為n2，從而得P2=n2﹣2n，根據題意假設存在，即n2﹣2n=5×2n，解之即可得出答案.
一本好題口算題卡系列答案科目：初中數學 來源： 題型：
【題目】如圖，EF∥AD，∠1 =∠2，∠BAC = 75°將求∠AGD的過程填寫完整
解：∵EF∥AD
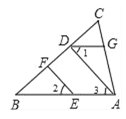
∴ ∠2 = （ ）
又∵ ∠1 = ∠2
∴ ∠1 = ∠3。（ ）
∴AB∥ 。（ ）
∴∠BAC + = 180°。（ ）
∵∠BAC=75°∴∠AGD = 。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在如圖所示的方格中，每個小方格都是邊長為1個單位長度的正方形，
的三個頂點都在格點（小方格的頂點）上．
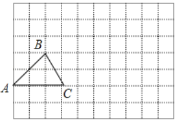
（1）請建立適當的平面直角坐標系，使
，
，并寫出點
的坐標；
（2）在（1）的條件下，將先向右平移4個單位長度再向上平移2個單位長度后可得到
，請在圖中畫出平移后的，并分別寫出點
，
，
的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩種型號的風扇成本分別為120元臺、170元臺,銷售情況如下表所示(成本、售價均保持不變,利潤=收入-成本)：
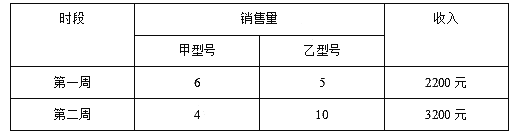
(1)求這兩種型號風扇的售價；
(2)該商場打算再采購這兩種型號的風扇共130臺，銷售完后總利潤能不能恰好為8010元?若能，給出相應的采購方案；若不能，說明理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1,點O是直線AB上的一點.
(1)如圖1,當∠AOD是直角,3∠AOC=∠BOD,求∠COD的度數；
(2)在(1)中∠COD繞著點O順時針旋轉(OD與OB重合即停止),如圖2，OE、OF分別平分∠AOC、∠BOD,則在旋轉過程中∠EOF的大小是否變化?若不變,求出∠EOF的大小；若改變,說明理由；
(3)在(1)中線段OC、OD繞著點O順時針旋轉,速度分別為每秒20°和每秒10°(當OD與OB重合時旋轉都停止),OM、ON分別平分∠BOC、∠BOD，多少秒時∠COM=∠BON(直接寫出答案,不必寫出過程).
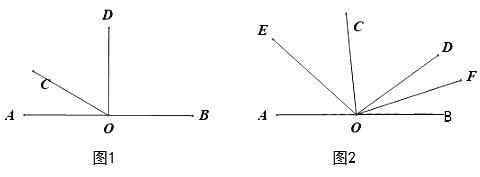
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，已知點
其中
滿足：
．
（1）
（2）在坐標平面內，將△ABC平移，點A的對應點為點D，點B的對應點為點E，點C的對應點為點F，若平移后E、F兩點都在坐標軸上，請直接寫出點E的坐標；
（3）若在△ABC內部的
軸上存在一點P，在（2）的平移下，點P的對應點為點Q，使得△APQ的面積為10，則點P的坐標為_________．
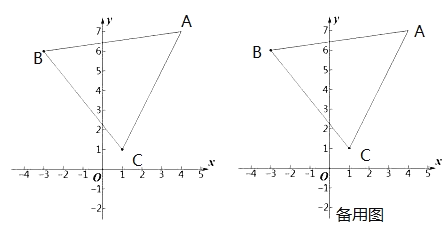
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P是射線BM上的一個動點(點P不與點B重合)，∠AOB= 30°，∠ABM=60°.當∠OAP=______時，以點A、O、B中的任意兩點和點P為頂點的三角形是等腰三角形.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，DE垂直平分AB ，分別交AB、BC于點D 、E，MN垂直平分AC，分別交AC、BC于點M、N，連接AE，AN.
(1)如圖1，若∠BAC= 100°，求∠EAN的度數；
(2)如圖2，若∠BAC=70°，求∠EAN的度數；
(3)若∠BAC=a(a≠90°)，請直接寫出∠EAN的度數. (用含a的代數式表示)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是老年活動中心門口放著的一個招牌，這個招牌是由三個特大號的骰子摞在一起而成的．每個骰子的六個面的點數分別是1到6，其中可以看見7個面，其余11個面是看不見的，則看不見的面上的點數總和是（ ）
A.41
B.40
C.39
D.38
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com