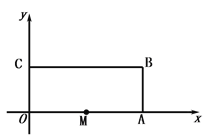
【題目】如圖，長方形OABC中，O為平面直角坐標系的原點，A點的坐標為（8，0），C點的坐標為（0，4），點B在第一象限內，點M從原點出發，以每秒2個單位長度的速度沿著O-A-B-C-O的路線移動（運動后到O點停止運動）．
（1）當點M移動了5秒時，點M的坐標是 ；
（2）在移動過程中，點M到y軸的距離為6個單位長度時，則點M移動的時間是 ；
（3）在移動過程中，若MB=MO，求點M移動的時間.
【答案】（1）（8，2）；（2）3s或7s；（3）
s和
s.
【解析】試題分析：（1）由時間及速度求出點M運動的路線長，根據點M沿著O-A-B-C-O的路線移動即可得出點M的位置；
（2）分類討論兩種情況：點M在OA上及點M在CB上通過時間＝路程÷速度即可得出答案；
（3）兩種情況：點M在OA上及點M在CB上，然后利用勾股定理即可求解.
解：（1）∵5×2＝10，且OA＝8，
∴點M運動到AB段上，且距點A：10-8＝2個單位長度，
∴點M的坐標是（8，2）.
故答案為：（8，2）.
（2）有兩種情況：
①當點在OA上時，M（6，0），
點M運動路程為6個單位長度，
∴運動時間為：6÷2＝3（s）；
②當點在BC上時，M（6，4），
點M運動路程為8+4+2＝14個單位長度，
∴運動時間為：14÷2＝7（s）；
故答案為：3s或7s.
（3）有兩種情況：
①當點M在OA上時，連接BM，
設OM＝a,則MB＝a，AM＝8-a,
在Rt△ABM中，由勾股定理得，
，
即， 
解得， 
所以OM＝5，
所以點M運動時間為： 
（s）；
②當點M在BC上時，連接BO，
同理可求BM＝5，
所以點M運動時間為： 
（s）；
故答案為： 
s和
s.
百強名校期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案
金狀元績優好卷系列答案科目：初中數學 來源： 題型：
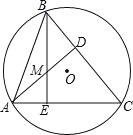
【題目】如圖，△ABC內接于⊙O，AD⊥BC，BE⊥AC，AD，BE相交于點M，若AC=8，BM=4，則⊙O的半徑等于（ ）
A．2
B．2
C．4
D．6
查看答案和解析>>
科目：初中數學 來源： 題型：
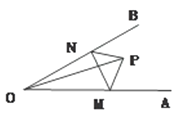
【題目】如圖，點P是∠AOB內任意一點，OP=4cm，點M和點N分別是射線OA和射線OB上的動點，∠AOB=30°則△PMN周長的最小值=________ .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】上星期我市某水果價格呈上升趨勢，某超市第一次用1000元購進的這種水果很快賣完，第二次又用960元購進該水果，但第二次每千克的進價是第一次進價的1.2倍，購進數量比第一次少了20千克．
（1）求第一次購進這種水果每千克的進價是多少元？
（2）本星期受天氣影響，批發市場這種水果的數量有所減少．該超市所購進的數量比上星期所進購的總量減少了4a%，每千克的進價在上星期第二次進價的基礎上上漲5a%，結果本星期進貨總額比上星期進貨總額少16元，求a的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
