【題目】（本小題滿分10分）如圖，一次函數
的圖象與反比例函數
（
為常數，且
）的圖象交于A（1，a）、B兩點．
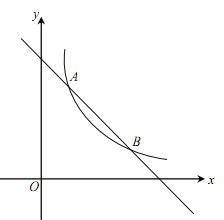
（1）求反比例函數的表達式及點B的坐標；
（2）在x軸上找一點P，使PA+PB的值最小，求滿足條件的點P的坐標及△PAB的面積．
【答案】（1）
，
；（2）P
，
．
【解析】
試題（1）由點A在一次函數圖象上，結合一次函數解析式可求出點A的坐標，再由點A的坐標利用待定系數法即可求出反比例函數解析式，聯立兩函數解析式成方程組，解方程組即可求出點B坐標；
（2）作點B作關于x軸的對稱點D，交x軸于點C，連接AD，交x軸于點P，連接PB．由點B、D的對稱性結合點B的坐標找出點D的坐標，設直線AD的解析式為y=mx+n，結合點A、D的坐標利用待定系數法求出直線AD的解析式，令直線AD的解析式中y=0求出點P的坐標，再通過分割圖形結合三角形的面積公式即可得出結論．
試題解析：（1）把點A（1，a）代入一次函數y=-x+4，
得：a=-1+4，解得：a=3，
∴點A的坐標為（1，3）．
把點A（1，3）代入反比例函數y=
，
得：3=k，
∴反比例函數的表達式y=
，
聯立兩個函數關系式成方程組得：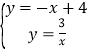
，
解得：
，或
，
∴點B的坐標為（3，1）．
（2）作點B作關于x軸的對稱點D，交x軸于點C，連接AD，交x軸于點P，此時PA+PB的值最小，連接PB，如圖所示．
∵點B、D關于x軸對稱，點B的坐標為（3，1），
∴點D的坐標為（3，- 1）．
設直線AD的解析式為y=mx+n，
把A，D兩點代入得：
，
解得：
，
∴直線AD的解析式為y=-2x+5．
令y=-2x+5中y=0，則-2x+5=0，
解得：x=
，
∴點P的坐標為（，0）．
S△PAB=S△ABD-S△PBD=
BD（xB-xA）-BD（xB-xP）
=×[1-（-1）]×（3-1）-×[1-（-1）]×（3-）
=
．
科目：初中數學 來源： 題型：
【題目】在一個不透明的盒子里有5個小球，分別標有數字﹣3，﹣2，﹣1，﹣
，﹣
，這些小球除所標的數不同外其余都相同，先從盒子隨機摸出1個球，記下所標的數，再從剩下的球中隨機摸出1個球，記下所標的數．
（1）用畫樹狀圖或列表的方法求兩次摸出的球所標的數之積不大于1的概率．
（2）若以第一次摸出球上的數字為橫坐標，第二次摸出球上的數字為縱坐標確定一點，直接寫出該點在雙曲線y=
上的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校部分團員參加社會公益活動，準備購進一批許愿瓶進行銷售，并將所得利潤捐給慈善機構.根據市場調查，這種許愿瓶一段時間內的銷售量y（個）與銷售單價x（元/個）之間的對應關系如圖所示：
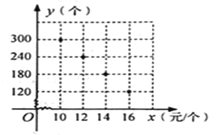
（1）試判斷y與x之間的函數關系，并求出函數關系式；
（2）若許愿瓶的進價為6元/個，按照上述市場調查的銷售規律，求銷售利潤w（元）與銷售單價x（元/個）之間的函數關系式；
（3）在（2）的條件下，若許愿瓶的進貨成本不超過900元，要想獲得最大的利潤，試確定這種許愿瓶的銷售單價，并求出此時的最大利潤.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ACB＝90°，點D、E分別在AB、AC上，且CE＝BC，連接CD，將線段CD繞點C按順時針方向旋轉90°后得到CF，連接EF．
（1）求證：△BDC≌△EFC；
（2）若EF∥CD，求證：∠BDC＝90°．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】人們在長期的數學實踐中總結了許多解決數學問題的方法，形成了許多光輝的數學想法，其中轉化思想是中學教學中最活躍，最實用，也是最重要的數學思想，例如將不規則圖形轉化為規則圖形就是研究圖形問題比較常用的一種方法．
問題提出：求邊長分別為、
、
、
的三角形面積．
問題解決：
在解答這個問題時，先建立一個正方形網格（每個小正方形的邊長為1），再在網格中畫出邊長分別為
、、的格點三角形
（如圖），
是角邊為1和2的直角三角形斜邊，
是直角邊分別為1和3的直角三角形的斜邊，
是直角邊分別為2和3的直角三角形斜邊，用一個大長方形的面積減去三個直角三角形的面積，這樣不需求的高，而借用網格就能計算它的面積.
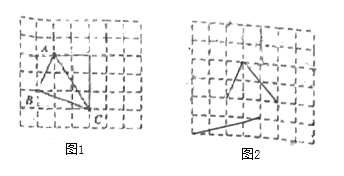
（1）請直接寫出圖①中的面積為____________.
（2）類比遷移：求邊長分別為、
、
的三角形面積（請利用圖②的正方形網格畫出相應的，并求出它的面積）
（3）思維拓展：求邊長分別為
，的三角形的面積
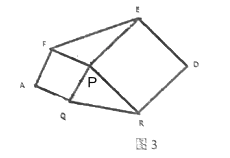
（4）如圖（3），已知
，以
，
為邊向外作正方形
，正方形
，連接
，若
，則六邊形 
的面積是_________.
查看答案和解析>>
科目：初中數學 來源： 題型：
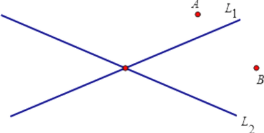
【題目】如圖，A、B是兩個工廠，L1、L2是兩條公路，現要在這一地區建一加油站，要求加油站到A、B兩廠的路程相等，且到兩條路的距離相等，請用尺規作圖找出符合條件的點P．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小王是“新星廠”的一名工人，請你閱讀下列信息：
信息一：工人工作時間：每天上午8：00—12：00，下午14：00—18：00，每月工作25天；
信息二：小王生產甲、乙兩種產品的件數與所用時間的關系見下表：
生產甲種產品數(件) | 生產乙種產品數(件) | 所用時間(分鐘) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三：按件計酬，每生產一件甲種產品得1.50元，每生產一件乙種產品得2.80元；
信息四：該廠工人每月收入由底薪和計酬工資兩部分構成，小王每月的底薪為1900元．請根據以上信息，解答下列問題：
(1)小王每生產一件甲種產品和一件乙種產品分別需要多少分鐘；
(2)2018年1月工廠要求小王生產甲種產品的件數不少于60件，則小王該月收入最多是多少元？此時小王生產的甲、乙兩種產品分別是多少件？
查看答案和解析>>
科目：初中數學 來源： 題型：
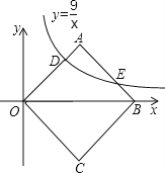
【題目】如圖，Rt△AOB中，∠OAB=90°，OA=AB，將Rt△AOB放置于直角坐標系中，OB在x軸上，點O是原點，點A在第一象限．點A與點C關于x軸對稱，連結BC，OC．雙曲線
(x＞0)與OA邊交于點D、與AB邊交于點E．
(1)求點D的坐標；
(2)求證：四邊形ABCD是正方形；
(3)連結AC交OB于點H，過點E作EG⊥AC于點G，交OA邊于點F，求四邊形OHGF的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們知道：等腰三角形兩腰上的高相等．
（1）請你寫出它的逆命題：______．
（2）逆命題是真命題嗎？若是，請證明；若不是，請舉出反例（要求：畫出圖形，寫出已知，求證和證明過程）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com