【題目】如圖，已知第一象限的點A在反比例函數y＝
上，過點A作AB⊥AO交x軸于點B，∠AOB＝30°，將△AOB繞點O逆時針旋轉120°，點B的對應點B恰好落在反比例函數y＝
上，則k的值為（ ）
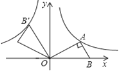
A.﹣4
B.﹣
C.﹣2D.﹣
名校課堂系列答案科目：初中數學 來源： 題型：
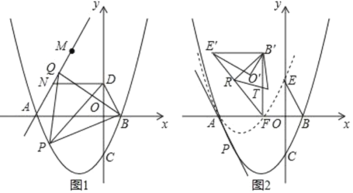
【題目】如圖，在平面直角標系中，拋物線C：y＝
與x軸交于A、B兩點（點A在點B的左側），與y軸交于點C，點D為y軸正半軸上一點．且滿足OD＝
OC，連接BD，
（1）如圖1，點P為拋物線上位于x軸下方一點，連接PB，PD，當S△PBD最大時，連接AP，以PB為邊向上作正△BPQ，連接AQ，點M與點N為直線AQ上的兩點，MN＝2且點N位于M點下方，連接DN，求DN+MN+
AM的最小值
（2）如圖2，在第（1）問的條件下，點C關于x軸的對稱點為E，將△BOE繞著點A逆時針旋轉60°得到△B′O′E′，將拋物線y＝沿著射線PA方向平移，使得平移后的拋物線C′經過點E，此時拋物線C′與x軸的右交點記為點F，連接E′F，B′F，R為線段E’F上的一點，連接B′R，將△B′E′R沿著B′R翻折后與△B′E′F重合部分記為△B′RT，在平面內找一個點S，使得以B′、R、T、S為頂點的四邊形為矩形，求點S的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
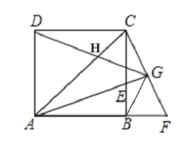
【題目】如圖，ABCD為正方形，∠CAB的角平分線交BC于點E，過點C作CF⊥AE交AE的延長線于點G，CF與AB的延長線交于點F，連接BG、DG、與AC相交于點H，則下列結論：①
ABE
CBF；②GF=CG；③BG⊥DG；④
，其中正確的是______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，BC是⊙O的切線，D是⊙O上的一點，且AD//CO．
（1）求證：△ADB∽△OBC；
（2）若AB=2，BC=
，求AD的長．（結果保留根號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】十八大以來，某校已舉辦五屆校園藝術節.為了弘揚中華優秀傳統文化，每屆藝術節上都有一些班級表演“經典誦讀”、“民樂演奏”、“歌曲聯唱”、“民族舞蹈”等節目.小穎對每屆藝術節表演這些節目的班級數進行統計，并繪制了如圖所示不完整的折線統計圖和扇形統計圖.
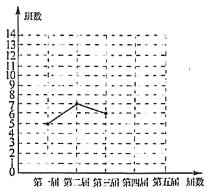
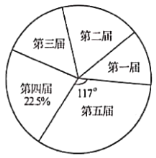
(1)五屆藝術節共有________個班級表演這些節日，班數的中位數為________，在扇形統計圖中，第四屆班級數的扇形圓心角的度數為________；
(2)補全折線統計圖；
(3)第六屆藝術節，某班決定從這四項藝術形式中任選兩項表演(“經典誦讀”、“民樂演奏”、“歌曲聯唱”、“民族舞蹈”分別用
，
，
，
表示).利用樹狀圖或表格求出該班選擇和兩項的概率.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】操作發現：如圖，已知△ABC和△ADE均為等腰三角形，AB＝AC，AD＝AE，將這兩個三角形放置在一起，使點B，D，E在同一直線上，連接CE．
（1）如圖1，若∠ABC＝∠ACB＝∠ADE＝∠AED＝55°，求證：△BAD≌△CAE；
（2）在（1）的條件下，求∠BEC的度數；
拓廣探索：（3）如圖2，若∠CAB＝∠EAD＝120°，BD＝4，CF為△BCE中BE邊上的高，請直接寫出EF的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】攀枝花得天獨厚，氣候宜人，農產品資源極為豐富，其中晚熟芒果遠銷北上廣等大城市．某水果店購進一批優質晚熟芒果，進價為10元/千克，售價不低于15元/千克，且不超過40元/每千克，根據銷售情況，發現該芒果在一天內的銷售量
（千克）與該天的售價
（元/千克）之間的數量滿足如下表所示的一次函數關系．
銷售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售價 | … | 27.5 | 25 | 24.5 | 22 | … |
（1）某天這種芒果售價為28元/千克．求當天該芒果的銷售量
（2）設某天銷售這種芒果獲利
元，寫出與售價之間的函數關系式．如果水果店該天獲利400元，那么這天芒果的售價為多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=ax2+bx﹣3a經過點A（﹣1，0）、C（0，3），與x軸交于另一點B，拋物線的頂點為D．
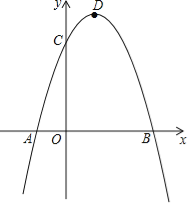
（1）求此二次函數解析式；
（2）連接DC、BC、DB，求證：△BCD是直角三角形；
（3）在對稱軸右側的拋物線上是否存在點P，使得△PDC為等腰三角形？若存在，求出符合條件的點P的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（12分）如圖1，點O是正方形ABCD兩對角線的交點，分別延長OD到點G，OC到點E，使OG=2OD，OE=2OC，然后以OG、OE為鄰邊作正方形OEFG，連接AG，DE．
（1）求證：DE⊥AG；
（2）正方形ABCD固定，將正方形OEFG繞點O逆時針旋轉α角（0°＜α＜360°）得到正方形OE′F′G′，如圖2．
①在旋轉過程中，當∠OAG′是直角時，求α的度數；
②若正方形ABCD的邊長為1，在旋轉過程中，求AF′長的最大值和此時α的度數，直接寫出結果不必說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
