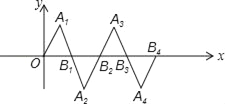
【題目】在如圖所示的平面直角坐標系中，△OA1B1是邊長為2的等邊三角形，作△B2A2B1與△OA1B1關于點B1成中心對稱，再作△B2A3B3與△B2A2B1關于點B2成中心對稱，如此作下去，則△B2nA2n+1B2n+1（n是正整數）的頂點A2n+1的坐標是_____．
【答案】(4n+1，
)
【解析】
試題首先根據△OA1B1是邊長為2的等邊三角形，可得A1的坐標為（1，），B1的坐標為（2，0）；然后根據中心對稱的性質，分別求出點A2、A3、A4的坐標各是多少；最后總結出An的坐標的規律，求出A2n+1的坐標是多少即可．
解：∵△OA1B1是邊長為2的等邊三角形，
∴A1的坐標為（1，），B1的坐標為（2，0），
∵△B2A2B1與△OA1B1關于點B1成中心對稱，
∴點A2與點A1關于點B1成中心對稱，
∵2×2﹣1=3，2×0﹣=﹣，
∴點A2的坐標是（3，﹣），
∵△B2A3B3與△B2A2B1關于點B2成中心對稱，
∴點A3與點A2關于點B2成中心對稱，
∵2×4﹣3=5，2×0﹣（﹣）=，
∴點A3的坐標是（5，），
∵△B3A4B4與△B3A3B2關于點B3成中心對稱，
∴點A4與點A3關于點B3成中心對稱，
∵2×6﹣5=7，2×0﹣=﹣，
∴點A4的坐標是（7，﹣），
…，
∵1=2×1﹣1，3=2×2﹣1，5=2×3﹣1，7=2×3﹣1，…，
∴An的橫坐標是2n﹣1，A2n+1的橫坐標是2（2n+1）﹣1=4n+1，
∵當n為奇數時，An的縱坐標是，當n為偶數時，An的縱坐標是﹣，
∴頂點A2n+1的縱坐標是，
∴△B2nA2n+1B2n+1（n是正整數）的頂點A2n+1的坐標是（4n+1，）．
故答案為：（4n+1，）．
應用題作業本系列答案
暑假作業暑假快樂練西安出版社系列答案科目：初中數學 來源： 題型：
【題目】在矩形ABCD中，AB=4cm，BC=8cm,動點P從點A出發，以1cm/s的速度沿AB向點B運動，動點Q從點B出發，以2cm/s秒的速度沿BC向點C運動.P、Q分別從A、B同時出發，設運動時間為t秒.(如圖1)
（１）用含t的代數式表示下列線段長度：
①PB=__________cm,②QB=_____cm,③CQ=_________cm.
(2)當△PBQ的面積等于3
時，求t的值.
(3) (如圖2)，若E為邊CD中點，連結EQ、AQ.當以A、B、Q為頂點的三角形與△EQC相似時，直接寫出滿足條件的t的所有值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形ABCD的頂點A，B在x軸上，且關于y軸對稱，反比例函數y=
（x＞0）的圖象經過點C，反比例函數y=
（x＜0）的圖象分別與AD，CD交于點E，F，若S△BEF=7，k1+3k2=0，則k1等于_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，把長方形紙片ABCD沿EF折疊后，使得點D與點B重合，點C落在點C′的位置上．
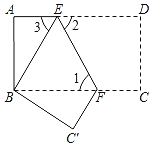
（1）折疊后，DC的對應線段是 ，CF的對應線段是 ．
（2）若∠1＝55°，求∠2、∠3的度數；
（3）若AB＝6，AD＝12，求△BC′F的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線y＝k1x＋b與雙曲線y＝
相交于A(1,2)、B(m，－1)兩點．
(1)求直線和雙曲線的解析式；
(2)若A1(x1，y1)、A2(x2，y2)、A3(x3，y3)為雙曲線上的三點，且x1＜x2＜0＜x3，請直接寫出y1、y2、y3的大小關系式；
(3)觀察圖象，請直接寫出不等式k1x＋b＞的解集．
查看答案和解析>>
科目：初中數學 來源： 題型：
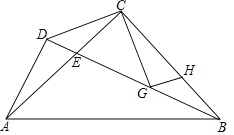
【題目】如圖△ABC中，CA＝CB，∠ACB＝90°，D為△ABC外一點，且AD⊥BD，BD交AC于E，G為BC上一點，且∠BCG＝∠DCA，過G點作GH⊥CG交CB于H．
（1）求證：CD＝CG；
（2）若AD＝CG，求證：AB＝AC+BH．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】據醫學研究,使用某種抗生素治療心肌炎,人體內每毫升血液中的含藥量不少于4微克時,治療有效.如果一患者按規定劑量服用這種抗生素,服用后每毫升血液中的含藥量
(微克)與服用后的時間
(小時)之間的函數關系如圖所示:
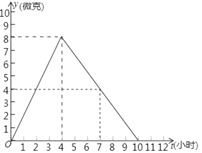
(1)如果上午8時服用該藥物,到 時該藥物的濃度達到最大值 微克/毫升;
(2)根據圖象求出從服用藥物起到藥物濃度最高時y與t之間的函數解析式;
(3)如果上午8時服用該藥物,到 時該藥物開始有效，有效時間一共是 小時;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
