

 ,
, ,則△BDC為Rt△;又∵E是BC的中點 ∴DE是Rt△BDC斜邊上的中線,所以DE=CE,所以
,則△BDC為Rt△;又∵E是BC的中點 ∴DE是Rt△BDC斜邊上的中線,所以DE=CE,所以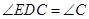 ;∵OA="OD" ∴
;∵OA="OD" ∴ ;如圖,Rt△ABC中,∠ABC=90°則
;如圖,Rt△ABC中,∠ABC=90°則 ,即
,即 ,所以
,所以 ,∴DE與⊙O相切
,∴DE與⊙O相切 ,∴
,∴ ;∵E是BC的中點,∴BC=2CE=8;若⊙O半徑r=3,則AB=2r=6;,Rt△ABC中由勾股定理得AC=10;根據三角形的面積相等得
;∵E是BC的中點,∴BC=2CE=8;若⊙O半徑r=3,則AB=2r=6;,Rt△ABC中由勾股定理得AC=10;根據三角形的面積相等得 ;解得BD=4.8; Rt△ABD中由勾股定理得
;解得BD=4.8; Rt△ABD中由勾股定理得


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com