
【題目】在![]() 中,
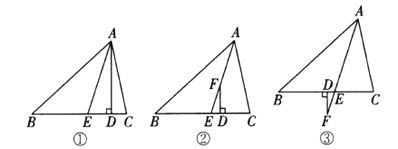
中,![]() .如圖①,
.如圖①,![]() 于點
于點![]() ,
,![]() 平分
平分![]() ,則易知
,則易知![]() .
.
(1)如圖②,![]() 平分
平分![]() ,
, ![]() 為
為![]() 上的一點,且
上的一點,且![]() 于點
于點![]() ,這時
,這時![]() 與
與![]() 、
、![]() 有何數量關系?請說明理由;
有何數量關系?請說明理由;
(2)如圖③,![]() 平分
平分![]() ,
,![]() 為
為![]() 延長線上的一點,
延長線上的一點,![]() 于點
于點![]() ,請你寫出這時
,請你寫出這時![]() 與
與![]() 、
、![]() 之間的數量關系(只寫結論,不必說明理由).
之間的數量關系(只寫結論,不必說明理由).
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)由角平分線的性質和三角形的內角和得出∠BAE=90°-![]() (∠C+∠B),外角的性質得出∠AEC=90°+
(∠C+∠B),外角的性質得出∠AEC=90°+![]() (∠B-∠C),在△EFD中,由三角形內角和定理可得∠EFD;
(∠B-∠C),在△EFD中,由三角形內角和定理可得∠EFD;
(2)由角平分線的性質和三角形的內角和得出∠BAE=90°-![]() (∠C+∠B), 外角的性質得出∠DEF=90°+
(∠C+∠B), 外角的性質得出∠DEF=90°+![]() (∠B-∠C), 在△EFD中,由三角形內角和定理可得∠EFD;
(∠B-∠C), 在△EFD中,由三角形內角和定理可得∠EFD;
試題解析:
∠EFD=![]() (∠C-∠B),理由如下:
(∠C-∠B),理由如下:
∵AE平分∠BAC,
∴∠BAE=![]() =90°-
=90°-![]() (∠C+∠B),
(∠C+∠B),
∵∠AEC為△ABE的外角,
∴∠AEC=∠B+90°-![]() (∠C+∠B)=90°+
(∠C+∠B)=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C)
(∠B-∠C)
∴∠EFD=![]() (∠C-∠B).
(∠C-∠B).
(2)∠EFD=![]() (∠C-∠B),理由如下:
(∠C-∠B),理由如下:
∵AE平分∠BAC,
∴∠BAE=![]() .
.
∵∠DEF為△ABE的外角,
∴∠DEF=∠B+![]() =90°+
=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C),
(∠B-∠C),
∴∠EFD=![]() (∠C-∠B).
(∠C-∠B).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
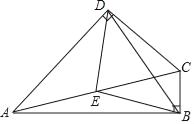
【題目】如圖,B、D、C三點在一條直線上,∠ADB=∠ADC=90°,BD=DE,∠DAC=45°;
(1)線段AB、CE的關系為 ;
(2)若BD=a,AD=b,AB=c,請利用此圖的面積式證明勾股定理.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在四邊形ABCD中,∠ABC=∠ADC=90°,點E是AC的中點.(1)求證:△BED是等腰三角形:
(2)當∠BCD=_____°時,△BED是等邊三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【新知理解】
如圖①,若點![]() 、
、![]() 在直線l同側,在直線l上找一點
在直線l同側,在直線l上找一點![]() ,使
,使![]() 的值最小.
的值最小.
作法:作點![]() 關于直線l的對稱點
關于直線l的對稱點![]() ,連接
,連接![]() 交直線l于點
交直線l于點![]() ,則點
,則點![]() 即為所求.
即為所求.
【解決問題】
如圖②,![]() 是邊長為6cm的等邊三角形
是邊長為6cm的等邊三角形![]() 的中線,點
的中線,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,則
上,則![]() 的最小值為 cm;
的最小值為 cm;
【拓展研究】
如圖③,在四邊形![]() 的對角線
的對角線![]() 上找一點
上找一點![]() ,使
,使![]() .(保留作圖痕跡,并對作圖方法進行說明)
.(保留作圖痕跡,并對作圖方法進行說明)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】游泳池常需進行換水清洗,圖中的折線表示的是游泳池換水清洗過程“排水—清洗—灌水”中水量y(m3)與時間t(min)之間的函數圖象.
(1)根據圖中提供的信息,求整個換水清洗過程水量y(m3)與時間t(min)的函數表達式;
(2)問排水、清洗、灌水各花多少時間?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級10個班師生舉行畢業文藝匯演,每班2個節目,有歌唱與舞蹈兩類節目,年級統計后發現歌唱類節目數比舞蹈類節目數的2倍少4個.
(1)九年級師生表演的歌唱與舞蹈類節目數各有多少個?
(2)該校七、八年級師生有小品節目參與,在歌唱、舞蹈、小品三類節目中,每個節目的演出平均用時分別是5分鐘、6分鐘、8分鐘,預計所有演出節目交接用時共花15分鐘.若從20:00開始,22:30之前演出結束,問參與的小品類節目最多能有多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,矩形ABCD的邊AB=3,AD=2,將此矩形置入直角坐標系中,使AB在x 軸上,點C 在直線y=x-2上.
(1)求矩形各頂點坐標;
(2)若直線y=x-2與y軸交于點E,拋物線過E、A、B三點,求拋物線的關系式;
(3)判斷上述拋物線的頂點是否落在矩形ABCD內部,并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com