
以原點(diǎn)O為圓心,1cm為半徑的圓分別交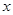 、
、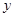 軸的正半軸于A、B兩點(diǎn),點(diǎn)P的坐標(biāo)為(2,0),動點(diǎn)Q從點(diǎn)B處出發(fā),沿圓周按順時針方向勻速運(yùn)動一周,設(shè)運(yùn)動的時間為秒.
軸的正半軸于A、B兩點(diǎn),點(diǎn)P的坐標(biāo)為(2,0),動點(diǎn)Q從點(diǎn)B處出發(fā),沿圓周按順時針方向勻速運(yùn)動一周,設(shè)運(yùn)動的時間為秒.
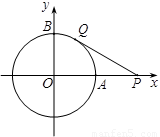
(1)如圖一,當(dāng)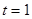 時,直線PQ恰好與⊙O第一次相切,連接OQ.求此時點(diǎn)Q的運(yùn)動速度(結(jié)果保留
時,直線PQ恰好與⊙O第一次相切,連接OQ.求此時點(diǎn)Q的運(yùn)動速度(結(jié)果保留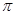 );
);
(2)若點(diǎn)Q按照(1)中的速度繼續(xù)運(yùn)動.
①當(dāng)為何值時,以O(shè)、P、Q為頂點(diǎn)的三角形是直角三角形;
②在①的條件下,如果直線PQ與⊙O相交,請求出直線PQ被⊙O所截的弦長.
(1)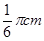 /秒;(2)①
/秒;(2)①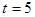 ,
,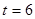 或
或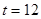 ;②
;②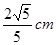
【解析】
試題分析:(1)連接OQ,則OQ⊥PQ,OQ=1,OP=2,所以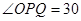 °,即
°,即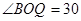 °,再根據(jù)弧長公式即可求得弧BQ的長,從而得到點(diǎn)Q的運(yùn)動速度;
°,再根據(jù)弧長公式即可求得弧BQ的長,從而得到點(diǎn)Q的運(yùn)動速度;
(2)①由(1)可知,當(dāng)t=1時,△OPQ為直角三角形,所以,當(dāng)Q'與Q關(guān)于x軸對稱時,△OPQ'為直角三角形,此時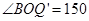 °,
°, ,
,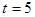 ,再結(jié)合當(dāng)Q'(0,-1)或Q'(0,1)時求解即可;
,再結(jié)合當(dāng)Q'(0,-1)或Q'(0,1)時求解即可;
②當(dāng)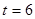 或
或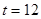 時,直線PQ與⊙O相交.作OM⊥PQ,根據(jù)等面積法及勾股定理可求得PM的長,從而求的結(jié)果.
時,直線PQ與⊙O相交.作OM⊥PQ,根據(jù)等面積法及勾股定理可求得PM的長,從而求的結(jié)果.
(1)連接OQ,
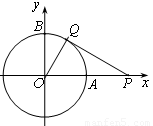
則OQ⊥PQ,OQ=1,OP=2,所以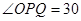 °,即
°,即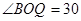 °,
°,
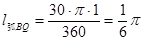 ,所以點(diǎn)Q的運(yùn)動速度為
,所以點(diǎn)Q的運(yùn)動速度為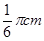 /秒;
/秒;
(2)①由(1)可知,當(dāng)t=1時,△OPQ為直角三角形,所以,當(dāng)Q'與Q關(guān)于x軸對稱時,△OPQ'為直角三角形,此時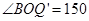 °,
°, ,
,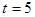 ,
,
當(dāng)Q'(0,-1)或Q'(0,1)時,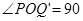 °,此時
°,此時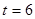 或
或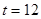 ,
,
即當(dāng)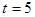 ,
,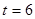 或
或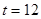 時,△OPQ是直角三角形;
時,△OPQ是直角三角形;
②當(dāng)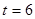 或
或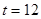 時,直線PQ與⊙O相交.作OM⊥PQ,根據(jù)等面積法可知:
時,直線PQ與⊙O相交.作OM⊥PQ,根據(jù)等面積法可知:
PQ×OM=OQ×OP,PQ=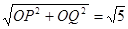 ,
,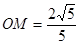 ,
,
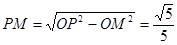 ,弦長
,弦長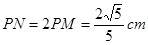 .
.
考點(diǎn):動點(diǎn)綜合題
點(diǎn)評:動點(diǎn)的綜合題是初中數(shù)學(xué)的重點(diǎn)和難點(diǎn),在中考中極為常見,一般壓軸題形式出現(xiàn),難度較大.


 黃岡創(chuàng)優(yōu)卷系列答案
黃岡創(chuàng)優(yōu)卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
 如圖,已知⊙O是以數(shù)軸的原點(diǎn)為圓心,半徑為1的圓,∠AOB=45°,點(diǎn)P在數(shù)軸上運(yùn)動,若過點(diǎn)P且與OB平行的直線于⊙O有公共點(diǎn),設(shè)P(x,0),則x的取值范圍是( )
如圖,已知⊙O是以數(shù)軸的原點(diǎn)為圓心,半徑為1的圓,∠AOB=45°,點(diǎn)P在數(shù)軸上運(yùn)動,若過點(diǎn)P且與OB平行的直線于⊙O有公共點(diǎn),設(shè)P(x,0),則x的取值范圍是( )| A、-1≤x<0或0<x≤1 | ||||
| B、0<x≤1 | ||||
C、-
| ||||
| D、x>1 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:單選題
 如圖,已知⊙O是以數(shù)軸的原點(diǎn)為圓心,半徑為1的圓,∠AOB=45°,點(diǎn)P在數(shù)軸上運(yùn)動,若過點(diǎn)P且與OB平行的直線于⊙O有公共點(diǎn),設(shè)P(x,0),則x的取值范圍是
如圖,已知⊙O是以數(shù)軸的原點(diǎn)為圓心,半徑為1的圓,∠AOB=45°,點(diǎn)P在數(shù)軸上運(yùn)動,若過點(diǎn)P且與OB平行的直線于⊙O有公共點(diǎn),設(shè)P(x,0),則x的取值范圍是 ≤x<0或0<x≤
≤x<0或0<x≤
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2011-2012學(xué)年江西省上饒市鄱陽縣九年級(上)期末數(shù)學(xué)試卷(解析版) 題型:選擇題

 ≤x<0或0<x≤
≤x<0或0<x≤
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2010-2011學(xué)年江西省南昌市九年級(上)期末數(shù)學(xué)試卷(解析版) 題型:選擇題

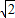 ≤x<0或0<x≤
≤x<0或0<x≤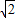
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com