
【題目】甲乙兩名戰士在相同條件下各射擊10次,每次命中的環數分別是:
甲:8,6,7,8,6,5,9,10,4,7 乙:6,7,7,6,7,8,7,9,8,5
(1)分別求出兩組數據的方差和標準差;
(2)根據計算結果,評價一下兩名戰士的射擊情況.
【答案】(1)![]() ,
,![]() ;
;![]() ,
,![]() ;(2)平均水平相同,乙射擊較穩定
;(2)平均水平相同,乙射擊較穩定
【解析】
(1)先求出甲和乙的平均數,再根據方差公式和標準差公式進行計算即可;
(2)依據甲乙兩人平均成績一樣,乙射擊成績的方差小于甲,即可得出乙的成績更加穩定.
解(1)∵![]() =
=![]() ×(8+6+7+8+6+5+9+10+4+7)=7,
×(8+6+7+8+6+5+9+10+4+7)=7,
∴![]() =
=![]() ×[(87)2+(67)2+(77)2+(87)2+(6-7)2+(57)2+(97)2+(107)2+(47)2+(77)2],
×[(87)2+(67)2+(77)2+(87)2+(6-7)2+(57)2+(97)2+(107)2+(47)2+(77)2],
=![]() ×(1+1+0+1+1+4+4+9+9+0),
×(1+1+0+1+1+4+4+9+9+0),
=3,
∴![]() ;
;
∵![]() =
=![]() ×(6+7+7+6+7+8+7+9+8+5)=7,
×(6+7+7+6+7+8+7+9+8+5)=7,
∴![]() =
=![]() ×[(67)2+(77)2+(77)2+(67)2+(7-7)2+(87)2+(77)2+(97)2+(87)2+(57)2],
×[(67)2+(77)2+(77)2+(67)2+(7-7)2+(87)2+(77)2+(97)2+(87)2+(57)2],
=![]() ×(1+0+0+1+0+1+0+4+1+4),
×(1+0+0+1+0+1+0+4+1+4),
=![]() ,
,
∴![]() ;
;
(2)∵![]() =
=![]() ,
,![]() <
<![]() ,
,
∴甲乙兩人平均成績一樣,乙射擊成績的方差小于甲,即可得出乙的成績更加穩定.


 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:初中數學 來源: 題型:
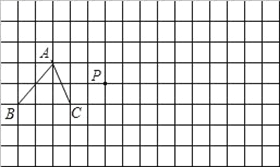
【題目】在下面16×8的正方形網格中,每個小正方形的邊長為1個單位,△ABC是格點三角形(頂點在網格交點處),請你畫出:
(1)△ABC的中心對稱圖形,A點為對稱中心;
(2)△ABC關于點P的位似△A′B′C′,且位似比為1:2;
(3)以A、B、C、D為頂點的所有格點平行四邊形ABCD的頂點D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新知認識:在△ABC中,∠A,∠B,∠C所對的邊分別用a,b,c表示,如果一個三角形的一個內角等于另一個內角的2倍,我們稱這樣的三角形為“倍角三角形”.
(1)特殊驗證:如圖1,在△ABC中,若a=![]() ,b=1,c=2,求證:△ABC為倍角三角形;
,b=1,c=2,求證:△ABC為倍角三角形;
(2)模型探究:如圖2,對于任意的倍角三角形,若∠A=2∠B,求證:a2=b(b+c)
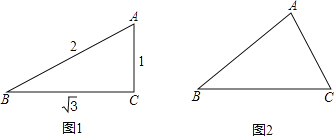
查看答案和解析>>
科目:初中數學 來源: 題型:
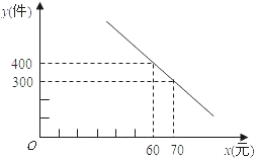
【題目】某服裝公司試銷一種成本為每件50元的T恤衫,規定試銷時的銷售單價不低于成本價,又不高于每件70元,試銷中銷售量y(件)與銷售單價x(元)的關系可以近似的看作一次函數(如圖).
(1)求y與x之間的函數關系式;
(2)設公司獲得的總利潤(總利潤=總銷售額-總成本)為P元,求P與x之間的函數關系式,并寫出自變量x的取值范圍;根據題意判斷:當x取何值時,P的值最大,最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用一根長22cm的鐵絲,
(1)能否圍成面積是30cm2的矩形?如果能,求出矩形的邊長,如果不能說明理由;
(2)能否圍成面積是32cm2的矩形?如果能,求出矩形的邊長,如果不能說明理由;
(3)請探索能圍成的矩形面積的最大值是多少 cm2?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場試銷一種成本為每件60元的服裝,規定試銷期間銷售單價不低于成本單價,且獲利不得高于45%,經試銷發現,銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元)符合一次函數
(元)符合一次函數![]() ,且
,且![]() 時,
時,![]() ;
;![]() 時,
時,![]() .
.
(1)求一次函數![]() 的表達式;
的表達式;
(2)若該商場獲得利潤為![]() 元,試寫出利潤
元,試寫出利潤![]() 與銷售單價
與銷售單價![]() 之間的關系式;銷售單價定為多少元時,商場可獲得最大利潤,最大利潤是多少元?
之間的關系式;銷售單價定為多少元時,商場可獲得最大利潤,最大利潤是多少元?
(3)若該商場獲得利潤不低于500元,試確定銷售單價![]() 的范圍.
的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于三角函數有如下的公式:
①cos(α+β)=cosαcosβ﹣sinαsinβ;sin(α+β)=sinαcosβ+cosαsinβ;
②tan(α+β)=![]() .
.
③利用這些公式可以將一些不是特殊角的三角函數轉化為特殊角的三角函數來求值,如tan105°=tan(45°+60°)=![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
根據上面的知識,你可以選擇適當的公式解決下面的實際問題:
(1)求cos75°的值;
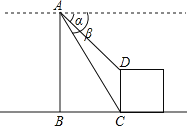
(2)如圖,直升機在一建筑物CD上方的點A處測得建筑物頂端點D的俯角α為60°,底端點C的俯角β為75°,此時直升機與建筑物CD的水平距離BC為42m,求建筑物CD的高.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知二次函數經過點B(3,0),C(0,3),D(4,-5)
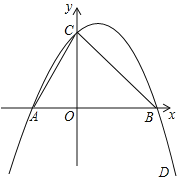
(1)求拋物線的解析式;
(2)求△ABC的面積;
(3)若P是拋物線上一點,且S△ABP=![]() S△ABC,這樣的點P有幾個請直接寫出它們的坐標.
S△ABC,這樣的點P有幾個請直接寫出它們的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
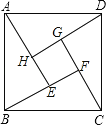
【題目】如圖,這個圖案是3世紀我國漢代數學家趙爽在注解《周髀算經》時給出的,人們稱它為“趙爽弦圖”.已知AE=3,BE=2,若向正方形ABCD內隨意投擲飛鏢(每次均落在正方形ABCD內,且落在正方形ABCD內任何一點的機會均等),則恰好落在正方形EFGH內的概率為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com