
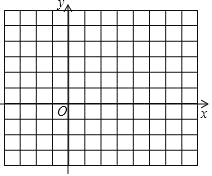
【題目】如圖,已知ABC 三個頂點的坐標分別為 A(2, 3) 、B(6, 0) 、C(1, 0)
(1)畫ABC ,直接寫出ABC 的面積 ;
(2)若A2 BC 與ABC 面積相等,則滿足條件的點 A2 有 個,它們的橫坐標為 ,縱坐標為 ;
(3)若A3 BC 與ABC 全等,請寫出滿足條件的 A3 的坐標.
【答案】(1)圖詳見解析,![]() ;(2)無數個,任意實數,3 或3 ;(3)A3 的坐標(6, 3) 或(2, 3) 或(6, 3) .
;(2)無數個,任意實數,3 或3 ;(3)A3 的坐標(6, 3) 或(2, 3) 或(6, 3) .
【解析】
(1)畫出△ABC,根據三角形的面積計算即可;
(2)若△A2BC與△ABC面積相等,則滿足條件的點A2在直線l1和直線l2上,由此即可解決問題;
(3)若△A3BC與△ABC全等,滿足條件的A3的坐標(6,3)或(-2,-3)或(6,-3);
(1)△ABC如圖所示.![]()
故答案為![]() .
.
(2)若△A2BC與△ABC面積相等,則滿足條件的點A2在直線l1和直線l2上,
∴則滿足條件的點A2有無數個個,它們的橫坐標為任意實數,縱坐標為3或3
故答案為無數個,任意實數,3或3;
(3)若△A3BC與△ABC全等,滿足條件的A3的坐標(6,3)或(2,3)或(6,3);


 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:初中數學 來源: 題型:
【題目】填空,完成下列說理過程
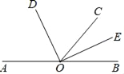
如圖,已知點A,O,B在同一條直線上,OE平分∠BOC,∠DOE=90°
求證:OD是∠AOC的平分線;
證明:如圖,因為OE是∠BOC的平分線,
所以∠BOE=∠COE.( )
因為∠DOE=90°
所以∠DOC+∠ =90°
且∠DOA+∠BOE=180°﹣∠DOE= °.
所以∠DOC+∠ =∠DOA+∠BOE.
所以∠ =∠ .
所以OD是∠AOC的平分線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖所示,∠5=∠CDA=∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:

∵∠5=∠CDA(已知),∴________∥________(內錯角相等,兩直線平行).
∵∠5=∠ABC(已知),∴________∥________(同位角相等,兩直線平行).
∵∠2=∠3(已知),∴________∥________(內錯角相等,兩直線平行).
∵∠BAD+∠CDA=180°(已知),
∴________∥________(同旁內角互補,兩直線平行).
∵∠5=∠CDA(已知),
又∠5與∠BCD互補,
∠CDA與________互補,
∴∠BCD=∠6(等角的補角相等),
∴________∥________(同位角相等,兩直線平行).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)a3(-b3)2+(-2ab2)3;
(2)(a-b)10÷(b-a)3÷(b-a)3;
(3)-22+(-![]() )-2-(π-5)0-|-4|;
)-2-(π-5)0-|-4|;
(4)(x+y-3)(x-y+3);
(5)3x2y(2x-3y)-(2xy+3y2)(3x2-3y);
(6)(x-2y)(x+2y)-(x-2y)2.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明對我校七年級(1)班喜歡什么球類運動的調查,下列圖形中的左圖是小明對所調查結果的條形統計圖.
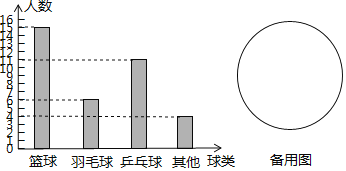
(1)問七年級(1)班共有多少學生?
(2)請你改用扇形統計圖來表示我校七年級(1)班同學喜歡的球類運動.
(3)從統計圖中你可以獲得哪些信息?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】湖州素有魚米之鄉之稱,某水產養殖大戶為了更好地發揮技術優勢,一次性收購了 ![]()
![]() 淡水魚,計劃養殖一段時間后再出售.已知每天放養的費用相同,放養
淡水魚,計劃養殖一段時間后再出售.已知每天放養的費用相同,放養 ![]() 天的總成本為
天的總成本為 ![]() 萬元;放養
萬元;放養 ![]() 天的總成本為
天的總成本為 ![]() 萬元(總成本=放養總費用+收購成本).
萬元(總成本=放養總費用+收購成本).
(1)設每天的放養費用是 ![]() 萬元,收購成本為
萬元,收購成本為 ![]() 萬元,求
萬元,求 ![]() 和
和 ![]() 的值;
的值;
(2)設這批淡水魚放養 ![]() 天后的質量為
天后的質量為 ![]() (
( ![]() ),銷售單價為
),銷售單價為 ![]() 元/
元/ ![]() .根據以往經驗可知:
.根據以往經驗可知: ![]() 與
與 ![]() 的函數關系為
的函數關系為 ![]() ;
; ![]() 與
與 ![]() 的函數關系如圖所示.
的函數關系如圖所示.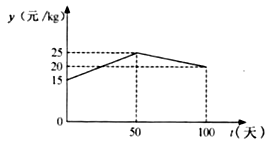
①分別求出當 ![]() 和
和 ![]() 時,
時, ![]() 與
與 ![]() 的函數關系式;
的函數關系式;
②設將這批淡水魚放養 ![]() 天后一次性出售所得利潤為
天后一次性出售所得利潤為 ![]() 元,求當
元,求當 ![]() 為何值時,
為何值時, ![]() 最大?并求出最大值.(利潤=銷售總額-總成本)
最大?并求出最大值.(利潤=銷售總額-總成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列結論:①AC﹣BE=AE;②點E在線段BC的垂直平分線上;③∠DAE=∠C;④BC=4AD,其中正確的有( )
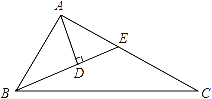
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=30°,將△ABC繞點B旋轉α(0<α<60°)到△A′BC′,邊AC和邊A′C′相交于點P,邊AC和邊BC′相交于Q.當△BPQ為等腰三角形時,則α=__________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com