
【題目】如圖, ![]() 為⊙
為⊙![]() 的直徑,
的直徑, ![]() 、
、![]() 分別是⊙
分別是⊙![]() 的切線,切點為
的切線,切點為![]() 、
、![]() ,
, ![]() 、
、![]() 的延長線交于點
的延長線交于點![]() ,
, ![]() ,交
,交![]() 的延長線于點
的延長線于點![]() .
.

(1)求證: ![]() ;
;
(2)若![]() ,
, ![]() ,求⊙
,求⊙![]() 的半徑.
的半徑.
【答案】(1)證明見解析;
(2)⊙![]() 的半徑
的半徑![]() .
.
【解析】(1)連接OC,易證∠DPO=∠BPO,∠BPO=∠EDB,故∠DPO=∠EDB
(2)在直角三角形PBD中,由PB與DB的長,利用勾股定理求出PD的長,由切線長定理得到PC=PB,由PD-PC求出CD的長,在直角三角形OCD中,設OC=r,則有OD=8-r,利用勾股定理列出關于r的方程,求出方程的解得到r的值,
試題解析:(1)連接OC,易證∠DPO=∠BPO,∠BPO=∠EDB
∴∠DPO=∠EDB

(2)在Rt△PBD中,PB=3,DB=4,
根據勾股定理得:PD=![]() ,
,
∵PD與PB都為圓的切線,
∴PC=PB=3,
∴DC=PD-PC=5-3=2,
在Rt△CDO中,設OC=r,則有DO=4-r,
根據勾股定理得:(4-r)2=r2+22,
解得:r=![]() .
.


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:
【題目】定義:點A(x,y)為平面直角坐標系內的點,若滿足x=y,則把點A叫做“平衡點”.例如:M(1,1),N(﹣2,﹣2)都是“平衡點”.當﹣1≤x≤3時,直線y=2x+m上有“平衡點”,則m的取值范圍是( )
A.0≤m≤1
B.﹣3≤m≤1
C.﹣3≤m≤3
D.﹣1≤m≤0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為1的正方形ABCD中,P為對角線AC上的任意一點,分別連接PB、PD,PE⊥PB,交CD與E,
(1)求證:PE=PD;
(2)當E為CD的中點時,求AP的長;
(3)設AP=x(![]() ),四邊形BPEC的面積為y,求證:
),四邊形BPEC的面積為y,求證: ![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
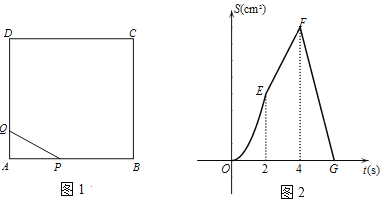
【題目】如圖1,四邊形![]() 是正方形,動點
是正方形,動點![]() 從點
從點![]() 出發,以
出發,以![]() cm/s的速度沿邊
cm/s的速度沿邊![]() 、
、![]() 、
、![]() 勻速運動到
勻速運動到![]() 終止;動點
終止;動點![]() 從
從![]() 出發,以
出發,以![]() cm/s的速度沿邊
cm/s的速度沿邊![]() 勻速運動到
勻速運動到![]() 終止,若
終止,若![]() 、
、![]() 兩點同時出發,運動時間為
兩點同時出發,運動時間為![]() s,△
s,△![]() 的面積為
的面積為![]() cm2.
cm2. ![]() 與
與![]() 之間函數關系的圖像如圖
之間函數關系的圖像如圖![]() 所示.
所示.
(1)求圖![]() 中線段
中線段![]() 所表示的函數關系式;
所表示的函數關系式;
(2)當動點![]() 在邊
在邊![]() 運動的過程中,若以
運動的過程中,若以![]() 、
、![]() 、
、![]() 為頂點的三角形是等腰三角形,求
為頂點的三角形是等腰三角形,求![]() 的值;
的值;
(3)是否存在這樣的![]() ,使
,使![]() 將正方形
將正方形![]() 的面積恰好分成
的面積恰好分成![]() 的兩部分?若存在,求出這樣的
的兩部分?若存在,求出這樣的![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() 的圖像與
的圖像與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,頂點
,頂點![]() 的橫坐標為
的橫坐標為![]() .
.

(1)求二次函數的表達式及![]() 的坐標;
的坐標;
(2)若![]() (
(![]() )是
)是![]() 軸上一點,
軸上一點, ![]() ,將點
,將點![]() 繞著點
繞著點![]() 順時針方向旋轉
順時針方向旋轉![]() 得到點
得到點![]() .當點
.當點![]() 恰好在該二次函數的圖像上時,求
恰好在該二次函數的圖像上時,求![]() 的值;
的值;
(3)在(2)的條件下,連接![]() .若
.若![]() 是該二次函數圖像上一點,且
是該二次函數圖像上一點,且![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種商品進價為a元,商店將價格提高30%作零售價銷售.在銷售旺季過后,商店又以8折(即售價的80%)的價格開展促銷活動.這時一件該商品的售價為( )
A.a元
B.0.8a元
C.1.04a元
D.0.92a元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:正方形ABCD的邊長為6,點E,F分別在邊AD,邊AB的延長線上,且DE=BF.
(1)如圖1,連接CE,CF,EF,請判斷△CEF的形狀;
(2)如圖2,連接EF交BD于M,當DE=2時,求AM的長;
(3)如圖3,點G,H分別在邊AB,邊CD上,且GH=3![]() ,當EF與GH的夾角為45°時,求DE的長.
,當EF與GH的夾角為45°時,求DE的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com